在完成陶哲轩 analysis 卷 ii, 4.7 三角函数之后就有一个问题困扰着我, 陶老师在这里通过级数定义的 sin/cos 与我初中时学过的通过几何形式定义的 sin/cos 是否是等价的? 当然答案肯定是等价的, 但如何证明是等价的一直困扰着我. 当时一直迫切于完成陶老师 analysis ii 所有章节的学习, 对这个问题没有深入探究下去. 现在在完成了 analysis ii 所有章节学习之后, 是时候再看下这个问题了.
可求长曲线, 首先参考鲁丁老师-数学分析原理第三版 6.5 节可求长曲线内容. 这块内容很直观, 拥有陶老师 analysis i/ii 卷经验的可以无障碍阅读, 这里就不复制内容过来了.
之后根据陶老师习题 15.7.4 可知, 如果 z 是复数, 且 z 的模为 1, 那么在 $(-\pi, \pi]$ 内存在唯一的 $\theta$, 使得 $z = \cos(\theta) + i\sin(\theta)$. 考虑到 sin/cos 周期性, 即在 $[0, 2\pi)$ 内存在唯一的 $\theta$. 令 $f(t) = (\cos(t), \sin(t)), t \in [0, 2\pi], f(t): R \to R^2$, 则 f(t) 是一个闭曲线, 它的值域是平面上的单位圆, 根据习题 15.7.4 可证对于单位圆上任意一点 $(x_0, y_0)$, 都存在唯一一个 t, 使得 $f(t) = (x_0, y_0)$.
此时 $f’(t) = (-\sin(t), \cos(t))$ 是连续的, 根据鲁丁老师定理 6.27 可知曲线 f(t) 是可求长的, 且在 $[0, t_0]$ 的曲线长为 $\int_0^{t_0}|f’(t)| dt = t_0$
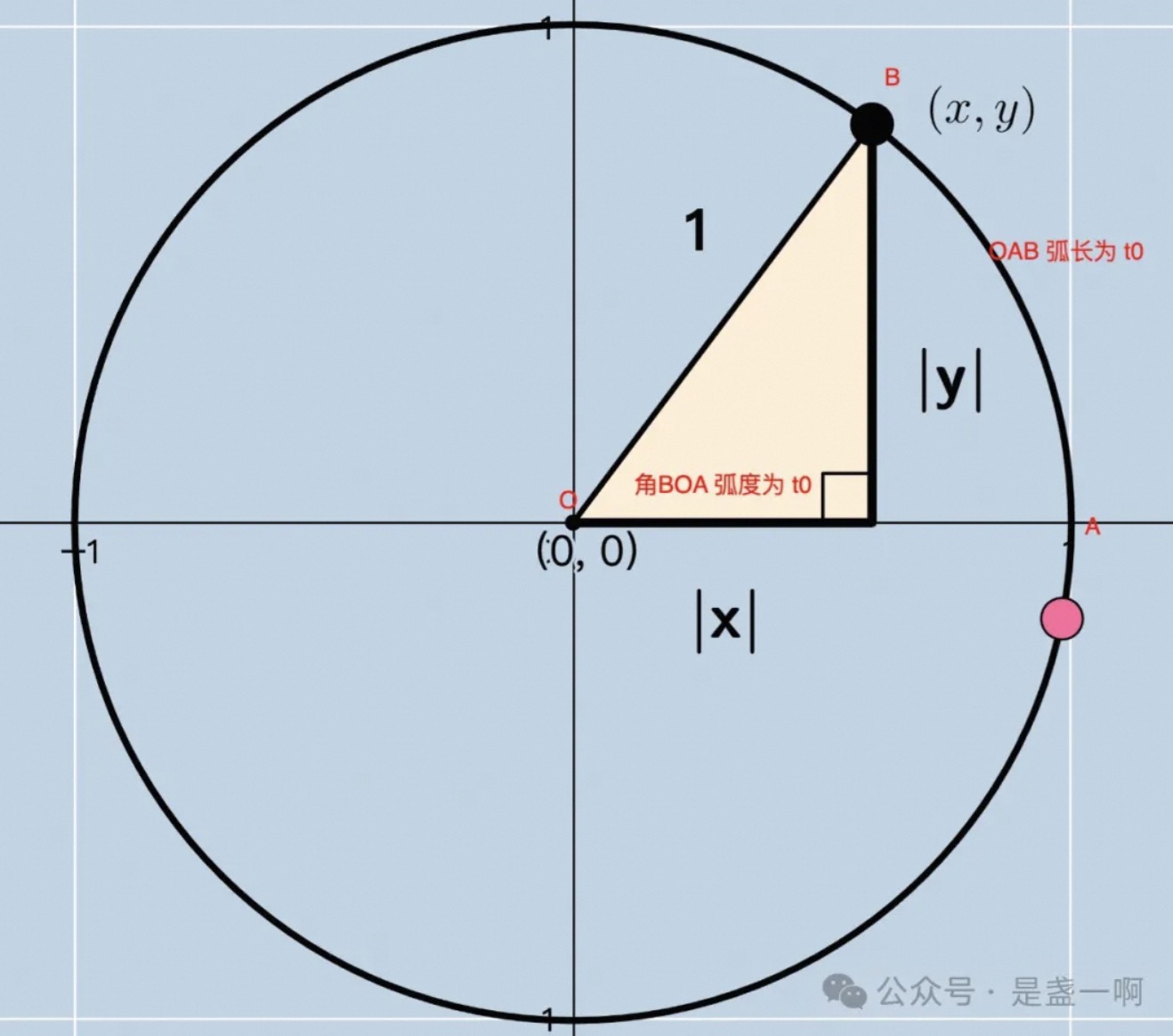
如图所示, 此时 A 点即 f(0) 对应的点, B 为 $f(t_0)$ 对应的点; 由曲线长公式可知 AB 弧长为 $t_0$, 根据角度弧度关系可知, 此时角 BOA 弧度值为 $t_0$. 根据我们初中所学可知此时 $\cos(t_0) = \frac{x}{1}, \sin(t_0) = \frac{y}{1}$. 而 x, y, 即 B 点坐标其分别是 $x = \cos(t_0), y = \sin(t_0)$.