这一篇文章介绍陶哲轩 analysis ii, 6.7 节多元微积分的反函数定理读书笔记.
习题 17.7.1,习题 6.7.1; f 是连续可微, 即 $f’$ 是连续的重要性, 若 $f’$ 不是连续的, 则意味着就算 $f’(x_0) > 0$, 那么 $\forall \delta, \exists x_1 \in [x_0 - \delta, x_0 + \delta], f’(x_1) < 0$. 史济怀数学分析教程定理 3.5.5 也举过一个例子, 对于这种函数, 任意小的区间, f 既不单调递增也不单调递减, 我当时还很好奇图像长啥样的.
引理 17.7.1, 我首先困惑的是线性变化总是可逆的吗? 实际上搜了下并不是. 所以这个引理完整描述应该是, 若 T 是可逆的, 则 T 的逆变化也是线性的.
定理 17.7.2, 反函数定理, 这里补充下若干细节.
- 如果 $f(x_0)$ 不可逆, 那么在 $f(x_0)$ 处逆映射 $f^{-1}$ 不可能存在, 也更不可能可微.
这句话首先 ‘如果 $f(x_0)$ 不可逆’ 应该是 ‘如果 $f’(x_0)$ 不可逆’. 另外即使 $f’(x_0)$ 不可逆, $f^{-1}$ 仍可能存在, 只不过不可能在 $f(x_0)$ 处可微. 如原文举的例子 $f(x) = x^3$ 就是这种. 我翻了下英文原文, 这里应该是翻译问题. 原话是:
We remark that this argument shows that if $f(x_0)$ is not invertible, then there is no way that an inverse $f^{-1}$ can exist and be differentiable at $f(x_0)$.
‘can exist and be differentiable’, 应该翻译成不可能存在一个在 $f(x_0)$ 处可微的逆函数.
- 假设我们已知了引理 1: 已知: $f: E \to R^n$, f 连续可微; $x_0 \in E, f(x_0) = 0, f’(x_0)$ 可逆. 则: $\exists U, x_0 \in U, \exists V, f(x_0) \in V$, $f: U \to V$ 是双射, 且 $f^{-1}$ 在 $f(x_0)$ 处可微. 求证原文定理 17.7.2
令 $\tilde{f}(x) = f(x) - f(x_0)$, 则 $\tilde{f}(x_0) = 0, \tilde{f}’(x) = f’(x), \tilde{f}(x)$ 符合引理 1 所有要求. 令 $V_f = {x + f(x_0), x \in V}$, 则易证 $V_f$ 是个开集. $f: U \to V_f$ 是个双射, 且 $f^{-1}(y) = \tilde{f}^{-1}(y - f(x_0))$. 此时 $f^{-1}$ 是 $\tilde{f}^{-1}$ 与 $g(y) = y - f(x_0)$ 的复合, 根据定理 17.4.1 可知 $ (f^{-1})’(y) = (\tilde{f}^{-1})’(y - f(x_0)), (f^{-1})’(f(x_0)) = (\tilde{f}^{-1})’(0) $.
- 假设我们已知了引理 2: 已知: $f: E \to R^n$, f 连续可微; $x_0 \in E, x_0 = 0, f(x_0) = 0, f’(x_0)$ 可逆. 则: $\exists U, x_0 \in U, \exists V, f(x_0) \in V$, $f: U \to V$ 是双射, 且 $f^{-1}$ 在 $f(x_0)$ 处可微. 求证引理 1.
令 $\tilde{f}(x) = f(x + x_0)$. 易证.
- 假设我们已知了引理 3: 已知: $f: E \to R^n$, f 连续可微; $x_0 \in E, x_0 = 0, f(x_0) = 0, f’(x_0) = I$. 则: $\exists U, x_0 \in U, \exists V, f(x_0) \in V$, $f: U \to V$ 是双射, 且 $f^{-1}$ 在 $f(x_0)$ 处可微. 求证引理 2.
令 $\tilde{f}(x) = (f’(0))^{-1}(f(x))$, 这里 $(f’(0))^{-1}$ 表示逆变换, 我老是觉得是 $\frac{1}{f’(0)}$, 则易证 $\tilde{f}’(x) = I$, 证明如下: 已知 f 在 $x_0 = 0$ 处可微, 即已知:
\[\lim_{x \to x_0}\frac{\lVert f(x) - f(x_0) - f'(x_0)(x - x_0) \rVert}{\lVert x - x_0 \rVert} = \lim_{x \to x_0}\frac{\lVert f(x) - f'(0)(x) \rVert}{\lVert x \rVert} = 0\]求证: $\lim_{x \to x_0}\frac{\lVert \tilde{f}(x) - \tilde{f}(x_0) - I(x - x_0) \rVert}{\lVert x - x_0 \rVert} = 0$.
\[\begin{align} \lim_{x \to x_0}\frac{\lVert \tilde{f}(x) - \tilde{f}(x_0) - I(x - x_0) \rVert}{\lVert x - x_0 \rVert} &= \lim_{x \to x_0}\frac{\lVert (f'(0))^{-1}(f(x)) - x \rVert}{\lVert x \rVert} \\ &= \lim_{x \to x_0}\frac{\lVert(f'(0))^{-1}(f(x) - f'(0)(x)) \rVert}{\lVert x \rVert} \end{align}\]根据习题 17.1.4, $\lVert(f’(0))^{-1}(f(x) - f’(0)(x)) \rVert \le M\lVert f(x) - f’(0)(x)\rVert$. 易证 $\lim_{x \to x_0}\frac{\lVert(f’(0))^{-1}(f(x) - f’(0)(x)) \rVert}{\lVert x \rVert} = 0$.
此时 $\tilde{f}(x)$ 符合引理 3 已知条件. $f(x) = f’(0)\tilde{f}(x), U_f = U_{\tilde{f}}, V_f = {f’(0)(x), x \in V_{\tilde{f}}}$, 此时易证 $V_{\tilde{f}}={f’(0)^{-1}(x), x \in V_f }, 0 \in V_f$, 并根据定理 13.1.5(c) 可知 $V_f$ 是开集. L1.
L1 标注: 在证明 $V_f$ 是开集上, 我一开始是 $V_{\tilde{f}}$ 是开集, $f’(0)$ 连续, 自然 $V_f$ 是开集; 即我认为连续性保证了开集. 但其实这一定理即习题 17.7.3 尚未证明,
- $g(y) - g(x) = \int_{0}^{1} \frac{d}{dt}g(x + t(y-x))dt$ 的推导.
令 $g = (g_1, \cdots, g_n), g_i(x) = f_i(x) - x_i$. 令 $F(t) = g(x + t(y-x)), R \to R^n$, 则 $F_i(t) = g_i(x + t(y-x)), R \to R$. 则有 $\int_0^1 \frac{d}{dt} F_i(t) = F_i(1) - F_i(0) = g_i(y) - g_i(x)$.
$\frac{d}{dt}g(x + t(y-x))$ 是个 $R \to R^n$ 映射, 则根据引理 16.4.4.zy2 有 $\int_{0}^{1} \frac{d}{dt}g(x + t(y-x))dt = (\int_{0}^{1} \frac{d}{dt}g_i(x + t(y-x))dt, \cdots)$
- $\frac{d}{dt}g(x + t(y-x)) = D_{y - x}g(x + t(y-x))$ 的证明
令 $F(t) = g(x + t(y-x)); h(t) = x + t(y-x), R \to R^n$. 由引理 17.2.1.zy2 可知 $\frac{d}{dt}F(t) = F’(t) = g’(x + t(y-x))h’(t)$. $h’(t) = \frac{dh}{dt} = (h_i’(t), \cdots) = (y_i - x_i, \cdots) = (y - x)$.
- $\frac{1}{2} \lVert x \rVert \le \lVert f(x) \rVert$ 的证明.
已知 $I = f - g, \lVert I \rVert \le \lVert f \rVert + \lVert g \rVert, \lVert f \rVert \ge \lVert I \rVert - \lVert g \rVert \ge \frac{1}{2} \lVert x \rVert $.
P.S. 我 I, f, g 排列组合试了好几次才找到这个正确的证明组合…
- 已知点列 $x^{(k)} \in R^n$, 则有 $\lim_{k \to \infty}x^{(k)} = 0$ 当且仅当 $\lim_{k \to \infty}\lVert x^{(k)} \rVert = 0$.
利用命题 12.1.18(d) 点列收敛等同于分量收敛. 结合不等式 $|x^{(k)}_i| \le \lVert x^{(k)}\rVert \le \sum_{i=0}^n|x^{(k)}_i|$
- $y_n$ 收敛于 0.
已知 $\lVert y_n \rVert \le 2 \lVert x_n \rVert$, 且 $\lim_{n \to \infty}\lVert x_n \rVert = 0$, 自然有 $\lim_{n \to \infty}\lVert y_n \rVert = 0$ 以及 $\lim_{n \to \infty} y_n = 0$.
- 证明 $\lim_{n \to \infty}\frac{\lVert f^{-1}(x_n) - x_n \rVert}{\lVert x_n \rVert} = 0$.
令 $y_n = f^{-1}(x_n)$, 则 $\lim_{n \to \infty}\frac{\lVert f^{-1}(x_n) - x_n \rVert}{\lVert x_n \rVert} = \lim_{n \to \infty}\frac{\lVert y_n - f(y_n) \rVert}{\lVert x_n \rVert}$. 已知 $y_n$ 收敛于 0, 且 f 在 0 处可微, 则 $\lim_{n \to \infty}\frac{\lVert f(y_n) - f(0) - f’(0)(y_n - 0) \rVert}{\lVert y_n \rVert} = 0$, 即 $\lim_{n \to \infty}\frac{\lVert f(y_n) - y_n \rVert}{\lVert y_n \rVert} = 0$; 这利用了命题 14.1.5(b).
$\frac{\lVert f^{-1}(x_n) - x_n \rVert}{\lVert x_n \rVert} = \frac{\lVert f(y_n) - y_n \rVert}{\lVert y_n \rVert} * \frac{\lVert y_n \rVert}{\lVert x_n \rVert}$, 且 $\frac{\lVert y_n \rVert}{\lVert x_n \rVert} \le 2$. 组合在一起易证结论.
习题 17.7.3, 习题 6.7.3; 我感觉原文证的有点不太完整. 我证明如下:
由反函数定理可知, $\forall x_0 \in V; \exists W_{x_0}’, x \in W_{x_0}’; \exists V_{x_0}’, f(x_0) \in V_{x_0}’$, $W_{x_0}’$, $V_{x_0}’$ 是开集, f 在 $W_{x_0}’$, $V_{x_0}’$ 之间是个双射. $f^{-1}$ 在 $V_{x_0}’$ 上连续; L1.
我这里本来有个比较麻烦的证明, 大致是令 $W_{x_0} = W_{x_0}’ \cap V$; 根据 12.2.15(f), 开集的交也是开集, 可知 $W_{x_0}$ 是个开集. $f(W_{x_0}) \subseteq V_{x_0}’ \cap f(V)$, 我本来试图证明 $f(W_{x_0}) = V_{x_0}’ \cap f(V)$, 但失败了. 此时 f 是 $W_{x_0}, f(W_{x_0})$ 之间一个双射, 且已知 $f^{-1}$ 在 $f(W_{x_0})$ 上连续, $W_{x_0}$ 是个开集, 根据定理 13.1.5(c) 可知 $f(W_{x_0})$ 也是个开集. 之后证明 $f(V) = \cup_{x_0 \in V}f(W_{x_0})$, 由 12.2.15(g) 任意开集的并也是开集得证 f(V) 也是个开集.
- L1, 我一开始以为这里原文证明 $f^{-1}$ 在 $V_{x_0}’$ 上连续的姿势不太对!
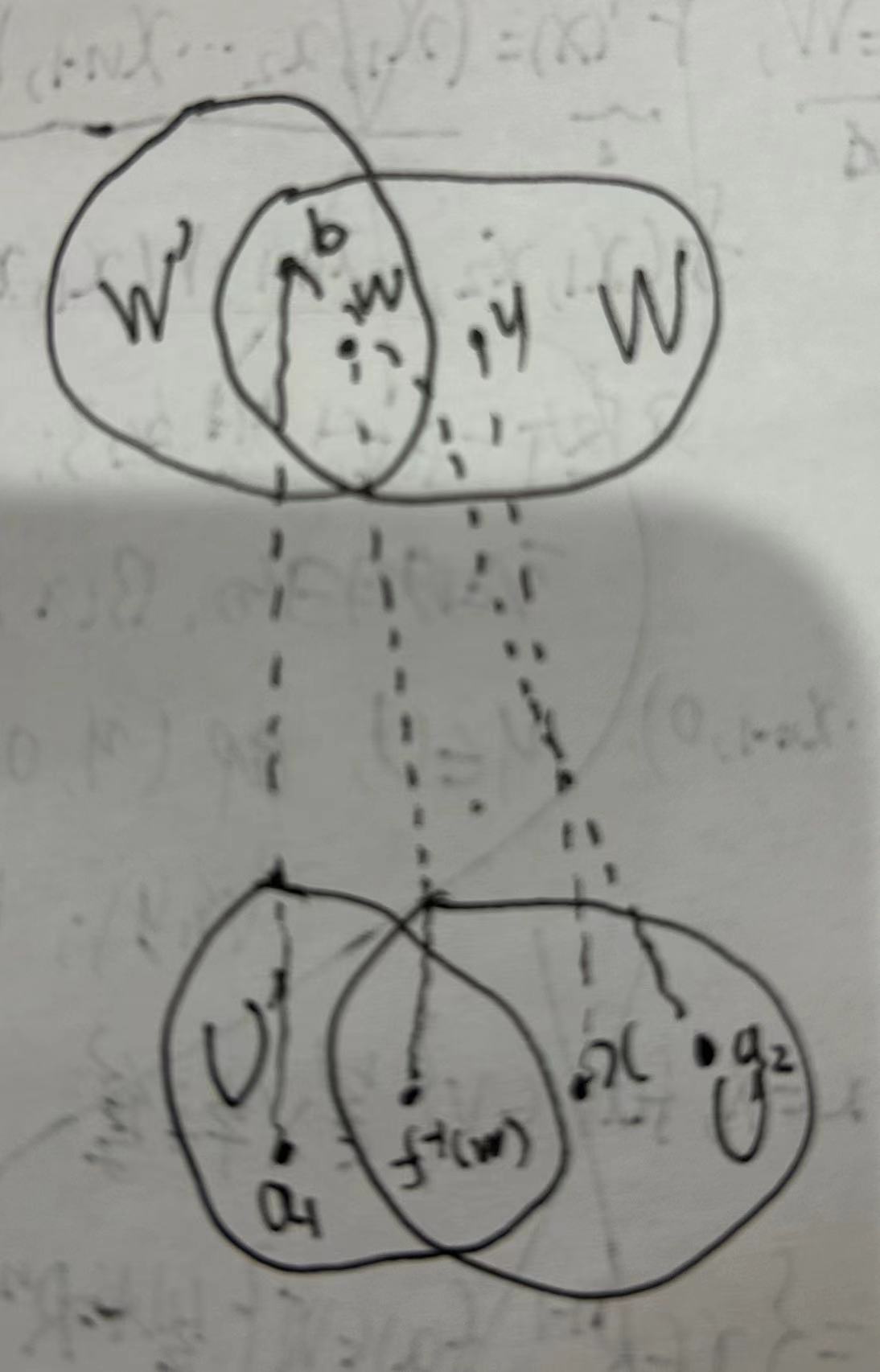
如上图所示, f 在 $f^{-1}(w)$ 可微且可逆, 则存在 $U’, W’$ 满足 f 双射; 问题是 $f^{-1}: W’ \to U’$ 与 $f^{-1}: W \to U$ 可能不是一个函数呀, 以图中点 b 为例, 其在 $W’$ 中映射到 $a_1 \in U’$, 在 W 中映射到 $a_2 \in U$.
但后来我意识到, 在利用反函数定理时, 可以把 U 这个开集认为是定理中的 E, 这样便能确保 $U’ \subseteq U, W’ \subseteq W$, 从而确保 $f^{-1}: W’ \to U’$ 与 $f^{-1}: W \to U$ 是同一个, 这样便可以了.
- 在接着上面开窍之后, 想到一个更简单的证明. 对于 $\forall y \in f(V), \exists x \in V; \exists r, B(x, r) \subseteq V$, 利用反函数定理, 将定理中的 E 认定为 B(x, r), 此时可知存在 U, W; U 是 B(x, r) 的子集; W 则是 f(V) 的子集, W 是开集, y 属于 W, 自然存在 y 的一个邻域是 W 的子集, 也是 f(V) 的子集. 这样 f(V) 便易证是开集了.