前言
如 无中生有的 nan 所示, 在我们很早之前为 vllm v1 引入 PD 分离之后, 紧接着要考虑的问题就是 PD 分离与引擎各个功能的适配问题, 比如与 SPS, 与 EP 等. 当然在我们早期设计 PD 分离时, 或者在为 vllm 引擎新增功能时, 就有原则:
目前我们的 PD 分离以及请求迁移都是在 EngineCore 上加了一些新接口(供我们内部组件调用), 并没有改变原有接口的逻辑, 而且我们新增接口在链路上尽可能复用了社区已有链路. 比如 PD 分离复用了 prompt cache 链路, 迁移复用了 preempt 链路(因为 preempt 可以视为单机内的迁移), 这意味着我们对引擎先有逻辑改动很少, 而且与其他功能(比如 sps, dp, ep等) 这些都不需要额外适配
所以实际上适配 SPS 并没有额外的开发工作, 只是需要做一些验证. 但我在扫描 Eagle 代码时发现如下片段, 即 input id 会丢掉 prompt first token 之后作为 draft model 输入:
# Shift the input ids by one token.
# E.g., [a1, b1, b2, c1, c2, c3] -> [b1, b2, c1, c2, c3, c3]
self.input_ids[:num_tokens - 1] = target_token_ids[1:]
# Replace the last token with the next token.
# E.g., [b1, b2, c1, c2, c3, c3] -> [a2, b2, b3, c2, c3, c4]
self.input_ids[last_token_indices] = next_token_ids
而我当时对 Eagle 一窍不通, 不由得幼稚发问:
Speculative Decoding
众所周知, 像 Transformers 这样的大型自回归模型在推理时速度较慢, 解码 K 个 token 需要对模型运行 K 次. 一个朴素的想法是引入一个小模型 draft model, 让小模型先自回归多次得到多个 token 之后作为输入运行一次大模型 target model 对多个 token 进行并行计算, 达到效果: 一次大型自回归模型的自回归可以生成多个 token. 作为该思路的开创性工作 Fast Inference from Transformers via Speculative Decoding 不仅提出了投机解码的方法, 还为其奠定了坚实的理论基础.
P.S. 这节我一开始想组织成一个流畅的故事, 从论文附录 A.1. Correctness of Speculative Sampling 证明出发, 一步步推导出 Algorithm 1 SpeculativeDecodingStep. 但感觉好像没有多大必要. 所以这一节还是按照我之前的习惯, 以 Q/A 的形式组织.
Q: 2.3 $x \sim p(x)$ 是什么意思?
A: 记住, 这里 $p(x)$ 是 $p(x_t \vert x_{\lt t})$, 即在给定输入 $x_{\lt t}$, LLM 生成的下一个 token $x_t$ 的分布. 这里 x 是个随机变量, 其表示下一个 token $x_t$. $p(x = i)$ 即下一个 token $x_t$ 取值为 token id i 的概率. $x \sim p(x)$ 即从分布 $p(x)$ 中选择下一个 token. 这里:
\[\begin{align} p(x) &= \left\{ p_1(x), p_2(x), \cdots, p_N(x) \right\} \\ q(x) &= \left\{ q_1(x), q_2(x), \cdots, q_N(x) \right\} \\ p'(x) &= norm(\max(0, p_i(x) - q_i(x))) \end{align}\]Q: Definition 3.2 的详细介绍?
A: 还是别忘了 $p(x)$ 是 $p(x_t \vert x_{\lt t})$, $q(x)$ 是 $q(x_t \vert x_{\lt t})$, p(x), q(x), M(x) 都可以视为 $1 \times N$ 的向量. $\sum_x \vert q(x) - M(x) \vert$ 就是 $\sum_{i=1}^N \vert q_i(x) - M_i(x) \vert$
Q: $\alpha = E(\beta)$ 怎么理解.
A: 这里 $\beta = \beta_{x_{\lt t}}$, 即在给定前缀 $x_{\lt t}$ 时, 小模型生成了分布 $q(x_t \vert x_{\lt t})$, 之后从这个分布中采样得到 $x_t$, 之后 $x_t$ 被大模型接受的概率. 这里 $x_{\lt t}$ 可以视为是个随机变量, $\beta$ 是随机变量 $x_{\lt t}$ 的函数, 其也是一个随机变量. $\alpha$ 则是在所有可能的前缀下, 随机变量 $\beta$ 的期望.
Q: Theorem 3.5 的进一步理解.
A: $\beta$ 是在给定前缀 $x_{\lt t}$ 时定义的, 所以下面讨论都是在给定前缀 $x_{\lt t}$ 时进行的, 这里 x 即随机变量 $x_t$, 其对应的分布 $q(x) = q(x_t \vert x_{\lt t})$. 随机变量 $f(x_t) = \begin{cases}
1, & q(x_t) \leq p(x_t)
\frac{p(x_t)}{q(x_t)}, & q(x_t) > p(x_t)
\end{cases}$ 为 $x_t$ 被接受的概率. 从定义上看 $\beta = E(f(x_t))$ 即 $x_t \sim q(x_t \vert x_{\lt t})$ 被接受的概率. 所以 $\beta = E(f(x_t)) = \sum_x f(x) q(x) = \sum_x \min(p(x), q(x))$.
Q: Corollary 3.6 的进一步理解.
A: $\alpha = E(\beta) = E(1 - D_{LK}(p, q))$, 这里 $D_{LK}(p, q)$ 为给定前缀 $x_{\lt t}$ 时确定的一个值, 即 $D_{LK}(p, q)$ 也是随机变量 $x_{\lt t}$ 的函数. $E(1 - D_{LK}(p, q)) = 1 - E(D_{LK}(p, q)) = E(\sum_x \min(p(x), q(x)))$. Qwen 说 $E(\min(p, q))$ 是 $E(\sum_x \min(p(x), q(x)))$ 的简写…
Q: Corollary 3.9 的理解.
A: 我本来以为这里是说在 $\alpha \gt c$ 的情况下, 必然存在 $\gamma$ 使得 $f(\gamma) = \frac{1 - \alpha^{\gamma + 1}}{(1 - \alpha)(\gamma c + 1)} \gt 1$. 但从证明过程来看并不是. 如下是不同 $\alpha, c$ 取值下, $f(\gamma)$ 的图像.
Q: A.1. Correctness of Speculative Sampling
A: 这里讨论都是在给定前缀 $x_{\lt t}$ 下进行的, 此时随机变量 x 为表示下一个 token $x_t$ 的值. $P(x = x’)$ 为在 2.3 节投机解码下随机变量 x 取值为 $x’$ 的概率. 我们要证明 $P(x = x’) = p(x = x’), \forall x’$ 成立, 这样才能说明投机解码没有改变大模型的输出分布.
在 Fast Inference from Transformers via Speculative Decoding 之后, 如 ‘Corollary 3.9 的理解’ 图像所示, 提升投机解码效果的主要两个手段就是: 提高 $\alpha$, 降低 $c$.
Eagle 3
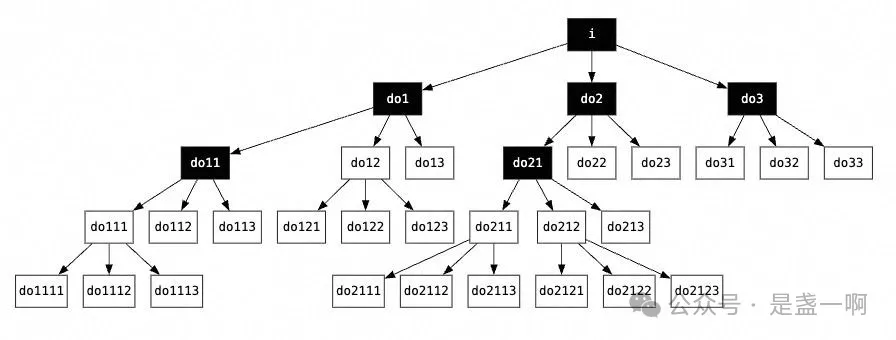
在 Eagle 3 中, draft model 核心由一个 Transformer decoder layer 组成, 其会基于 target model 的输出 top-layer features 进行训练, 我理解这样可以确保 draft model 更近似 target model, 即 $\alpha$ 可以很高. 同时基于 tree attention 构建了 tree-structured draft, 如 Eagle 论文图 6 所示, 可以在 3 次 forward 之后生成一个 10-token tree, 意味着 $c$ 被均摊之后会很小. 本节我们先不深入到具体代码, 而以一个具体的场景为例演示下 Eagle3 运行情况从而先有个直观认识. 该场景中: 用户输入 how can, top_k=3, depth=3, total_token=6. 在符号上会尽量使用原论文中的符号.
-
将用户输入
how can送入 target model, 得到 first tokeni. -
将 input_ids:
how can i, 与how can对应 target model 输出的 feature $h_{how}, m_{how}, l_{how}, h_{can}, m_{can}, l_{can}$ 作为输入送往 draft model, 此时 draft model 会先用一个 FC 将 $h_{how}, m_{how}, l_{how}, h_{can}, m_{can}, l_{can}$ 映射为 $g_{how}, g_{can}$, 之后将 $g_{how}, e_{can}$, $g_{can}, e_{i}$ 拼接在一起送往 draft model decode layer. 这里将输出记为 $a_{can}, a_{i}$, 之后从 $a_{i}$ 对应 logits 中采样 top_k=3 个候选, 假设是do1 do2 do3. 之后开始 depth 次 draft model forward.-
i=0 forward 输入 input_ids:
do1 do2 do3. input_hidden: $a_{i}, a_{i}, a_{i}$.# 对应 tree attention how can i do1 do2 do3 do1 o o o o x x do2 o o o x o x do3 o o o x x o输出 out_hidden $a_{do1}, a_{do2}, a_{do3}$.
# 先在每一行进行 top_k=3 采样, 这里列出被选中的 token. a_do1: do11 do12 do13 a_do2: do21 do22 do23 a_do3: do31 do32 do33 # 之后在 9 个被选中 token 中再进行 top_k=3 采样, # 假设选中了 [do21, do11, do12]. -
i=1 forward, 输入 input_ids:
do21, do11, do12. input_hidden:a_do2, a_do1, a_do1. 输出 out_hidden 相当于a_do21, a_do11, a_do12.# tree attention how can i do1 do2 do3 do21 do11 do12 do21 o o o x o x o x x do11 o o o o x x x o x do12 o o o o x x x x o # top k 采样, 选中了 [do111, do211, do212] a_do21: do211 do212 do213 a_do11: do111 do112 do113 a_do12: do121 do122 do123 -
i=2 forward, 输入 input_ids:
do111, do211, do212. input_hidden:a_do11, a_do21, a_do21. 输出 out_hidden 相当于a_do111 a_do211 a_do212.# tree attention how can i do1 do2 do3 do21 do11 do12 do111 do211 do212 do111 o o o o x x x o x o x x do211 o o o x o x o x x x o x do212 o o o x o x o x x x x o # top k 采样, 选中了 [do111, do211, do212] a_do111: do1111 do1112 do1113 a_do211: do2111 do2112 do2113 a_do212: do2121 do2122 do2123 -
depth=3 次 forward 生成的 draft tree 如下所示. 黑色背景意味着被 total_tokens 选中的 token.
-
-
之后将
i do1 do2 do3 do11 do21作为输入送往 target model 经一次 forward 来进行验证. 此时也会使用 tree attention.# attention mask. how can i do1 do2 do3 do11 do21 # kvcache i o o o x x x x x do1 o o o o x x x x do2 o o o x o x x x do3 o o o x x o x x do11 o o o o x x o x do21 o o o x o x x o # input如下 candidates 每一行就表示 draft tree 中从 sample token 到某个 leaf token 的一个路径.
# candidates i do3 -1 i do1 do11 i do2 do21这一步验证工作会确定选择接受哪个路径, 以及该路径前多少个 token. 假设验证结果选择接受路径
i do2 do21所有 token. 此时用户输入变为how can i do2 do21 do21',do21'为本轮验证时 target model 为do21选择的 next token. -
此时重新执行第 2 步, input_ids:
i do2 do21 do21', 与 target model 为i do2 do21生成的 feature 作为 draft model 输入. draft model 会丢掉输入的 first token 将 tokendo2 do21 do21'对应 embed 与i do2 do21生成的 feature 拼接在一起, 又一次开始一轮循环….
后记
所以回到最开始那个幼稚的问题: 礼貌一点会影响推理性能么? 答案是: 不会! 如 Eagle 论文 4.3.2Inputs of draft models 节所做消融实验所示: feature&shifted-token 会在各个角度取得不错的效果.