整理笔记时发现这篇之前学习 Gpipe 的总结, 略加梳理之后发表出来, 希望能帮到你=. =
关于前向传播, 后向传播, 以及 Gpipe 中 pipeline parallelism 一开始是囫囵吞枣地一股脑生咽下去的; 看似是懂了 gpipe, 但其实说到细节处总有点含含糊糊的地方. 现在正好有空, 总结梳理下. 本文假设你已经有 这里 提到的数学常识.
再次回到吴恩达老师在其 ‘Basics of Neural Network programming’ 中提到的单个神经元网络模型, 这里存在一个函数 $f(x)$, 其包含两个参数 $w, b$; 也即 $w, b$ 值确定时, 我们便得到了一个函数 $f_{w, b}(x)$, 给定一个 $x$ 带入该函数可得一个值 $y$. 现在有一坨样本 $x_i, y_i. i \in [1, m]$, 我们要做的是寻找 $w, b$ 使得代价函数 $J(w, b) = \frac{1}{m} \sum_{i=1}^m L(\hat{y_i}, y_i)$ 取值最小; 这里 $\hat{y_i}=f(x_i)$ 为样本 $x_i$ 带入 f 之后得到的预测值, $y_i$ 为样本 $x_i$ 对应的值. 具体做法也很直观:
- 随机初始化 $w_0, b_0$.
- 求取 $\frac{\partial J}{\partial w}, \frac{\partial J}{\partial b}$ 在点 $w_0, b_0$ 的取值, 并以此更新
- 计算 $J(w_0, b_0)$, 若此时代价不符合预期, 继续第二步迭代. 否则此时 $w_0, b_0$ 便是我们训练得到的模型参数, 如上可知我们以此确定了一个函数 $f_{w_0, b_0}(x)$, 后续便可以使用这个函数进行二分类工作.
P.S. 我一开始弄混了 $f, J$..
继续看吴恩达老师这张图, 正向传播便是在给定 $w_1^v, w_2^v, b^v$ 前提下, 如上所示此时确定了函数 f, 带入样本 x 依次得到值 $z^v, a^v$, 并得到了此时代价函数 $L(w_1^v, w_2^v, b^v)$ 的结果.

P.S. $w_1^v$ 表示参数 $w_1$ 的一次取值, 我发现这里区分清楚何时是参数, 何时是值有助于加深理解. 另外我实在找不到合适的符号了, 所以用了上标==
而反向传播, 核心是要计算偏导数 $\frac{\partial L}{\partial w_1}, \frac{\partial L}{\partial w_2}, \frac{\partial L}{\partial b}$ 在点 $(w_1^v, w_2^v, b^v)$ 的值, 并以此更新 $w_1^v, w_2^v, b^v$. 之后便使用 $w_1^v, w_2^v, b^v$ 更新后的值再开始一轮前向后向迭代. 在神经网络层数较多的情况下, 并不方便直接计算 $\frac{\partial L}{\partial w_1}$, 于是利用了链式法则来分解计算:
\[\begin{align} \frac{\partial L}{\partial w_1}(w_1^v, w_2^v, b^v) &= \frac{\partial L}{\partial z}(z^v) \frac{\partial z}{\partial w_1}(w_1^v, w_2^v, b^v) \\ \frac{\partial L}{\partial z}(z^v) &= \frac{\partial L}{\partial a} (a^v, y) \frac{\partial a}{\partial z}(z^v) \\ \frac{\partial L}{\partial a} (a^v, y) &= -\frac{y}{a^v} + \frac{1-y}{1- a^v} \end{align}\]在正向传播中, 我们计算出了 $a^v, y$ 根据如上公式在反向传播阶段我们依次计算 $\frac{\partial L}{\partial a} (a^v, y), \frac{\partial L}{\partial z}(z^v)$ 直到我们需要的 $\frac{\partial L}{\partial w_1}(w_1^v, w_2^v, b^v)$. 这里提一下链式法则, 还是那句话分清楚参数与值:
\[(g \circ f)'(x_0) = g'(f(x_0)) f'(x_0)\]P.S. 吴恩达老师习惯使用 $d_{w1}$ 来表示偏导数 $\frac{\partial L}{\partial w_1}$ 在点 $(w_1^v, w_2^v, b^v)$ 的值.
基于这个背景知识我们便可以比较容易地定义出神经网络的一个层在正向传播阶段的输入, 输出; 以及在反向传播阶段的输入, 输出. 如下图中 $(n^{[l]}, m)$ 表示对应矩阵的形状.
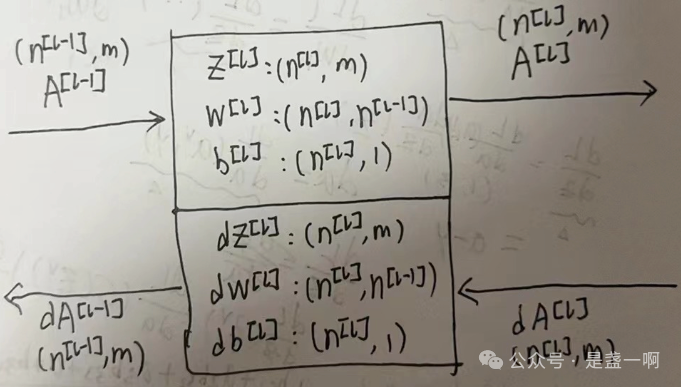
这样就很理解 Gpipe 2.1 Interface 节了. 接着是 2.2 Algorithm 节, Gpipe 这里将 mini-batch 化分为 micro-batch, 虽然训练是 micro-batch 粒度的, 但效果是完全等同于 mini-batch 的. 核心就在于:
At the end of each mini-batch, gradients from all M micro-batches are accumulated and applied to update the model parameters across all accelerators.
这里以上图为例来演示下这个过程, 假设这里 mini-batch, m = 4, micro-batch = 2.
\[\begin{align} dZ^{[2]} &= (a_1, a_2, a_3, a_4) \\ A^{[1]} &= \begin{pmatrix} b_{11} & b_{12} & b_{13} & b_{14} \\ b_{21} & b_{22} & b_{23} & b_{24} \\ b_{31} & b_{32} & b_{33} & b_{34} \\ \end{pmatrix} \\ dW^{[2]} = \frac{1}{m} dZ^{[2]} (A^{[1]})^T &= \begin{pmatrix} \frac{a_1 b_{11} + a_2 b_{12} + a_3 b_{13} + a_4 b_{14}}{4} \\ \frac{a_1 b_{21} + a_2 b_{22} + a_3 b_{23} + a_4 b_{24}}{4} \\ \frac{a_1 b_{31} + a_2 b_{32} + a_3 b_{33} + a_4 b_{34}}{4} \\ \end{pmatrix}^T \end{align}\]P.S. 这里 $dW^{[2]}$ 是 $1 \times 3$ 矩阵, 我为了美观将其画成 $3 \times 1$, 所以加了个转置符号=. =
将其切换为 2 个 micro-batch 之后, $dZ^{[2]}_1, dZ^{[2]}_2$ 分别表示第 1, 2 个 micro-batch 过程中 $dZ^{[2]}$ 的值. 这里很容易可以看到 $dW^{[2]} = dW^{[2]}_1 + dW^{[2]}_2$.
\[\begin{array}{ll} A^{[1]}_1 = \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \\ b_{31} & b_{32} \\ \end{pmatrix} & A^{[1]}_2 = \begin{pmatrix} b_{13} & b_{14} \\ b_{23} & b_{24} \\ b_{33} & b_{34} \\ \end{pmatrix} \\ dZ^{[2]}_1 = (a_1, a_2) & dZ^{[2]}_2 = (a_3, a_4) \\ dW^{[2]}_1 = \begin{pmatrix} \frac{a_1 b_{11} + a_2 b_{12}}{4} \\ \frac{a_1 b_{21} + a_2 b_{22}}{4} \\ \frac{a_1 b_{31} + a_2 b_{32}}{4} \\ \end{pmatrix}^T & dW^{[2]}_2 = \begin{pmatrix} \frac{a_3 b_{13} + a_4 b_{14}}{4} \\ \frac{a_3 b_{23} + a_4 b_{24}}{4} \\ \frac{a_3 b_{33} + a_4 b_{34}}{4} \\ \end{pmatrix}^T \end{array}\]P.S. 在计算 $dW^{[2]}_1$ 时, 我本来以为 $dW^{[2]} = \frac{1}{m} dZ^{[2]} (A^{[1]})^T$ 的 m 应该要调整为 micro-batch 的大小, 即 2. 但现在看来并不需要. 同理代价函数 $J(w, b) = \frac{1}{m} \sum_{i=1}^m L(\hat{y_i}, y_i)$ 也是如此 $J = J_1 + J_2$:
\[\begin{align} J_1 &= \frac{1}{4} (L(\hat{y_1}, y_1) + L(\hat{y_2}, y_2)) \\ J_2 &= \frac{1}{4} (L(\hat{y_3}, y_3) + L(\hat{y_4}, y_4)) \\ \end{align}\]所以就像 Gpipe 论文中提到的, Gpipe 完全不需要去改动模型内部代码.
再结合着对 pytorch DDP 实现学习之后再来看之前这篇描述, 可以发现理解有一点偏差. 假设 minibatch 大小为 $K$, micro-batch 大小为 $k, K = k n$. 在不划分 micro-batch 情况下:
\[dW = \frac{s_1 + \cdots + s_K}{K}\]在划分 micro-batch 时, 此时每个 micro-batch 对应
\[dW_i = \frac{s_{i1} + \cdots + s_{ik}}{k}\]即这里 $dW^{[2]} = \frac{1}{m} dZ^{[2]} (A^{[1]})^T$ 的 m 确实是应该要调整为 micro-batch 的大小的. 所以 $dW = \frac{1}{n}\sum_{i=1}^n dW_i$. 这也是 DDP 实现注释中提到的:
When this is done, averaged gradients are written to the param.grad field of all parameters.
参考
- Basics of Neural Network programming
- Shallow neural networks
- Deep Neural Networks
- Gpipe: Easy Scaling with Micro-Batch Pipeline Parallelism