系列导言, 本文是作者在学习 Peter D. Lax 线性代数及其应用的读书笔记, 侧重于记录我当时没有看懂的部分, 以及对书中部分知识点的一些扩展. 非常零散, 不成系统. 对本系列的使用最好是读者也在学习 Peter D. Lax 线代并且恰好有某处不太明白, 可以参考着本系列说不定这里就有答案. 本系列文章在写作时参考了互联网上零零散散非常多的资料在此表示感谢!
练习 8, $T’’ = T$ 证明, 结合图示看
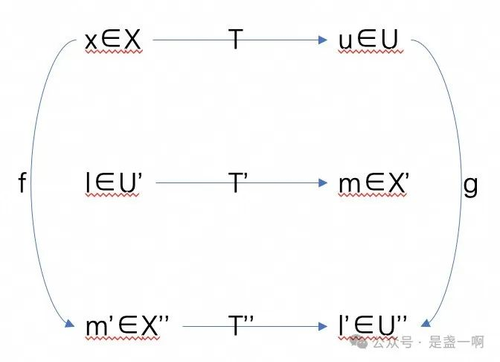
首先 $T’‘=T$ 是指什么, 这里我们知道 $T’’: X’’ \to U’’, T: X \to U$, 从常规的等号意义来看, 这俩是肯定不是一回事. 由第 2 章公式 5 可知 $\forall x \in X$, x 可以用 $(x_1, \cdots, x_n)$ n 个标量构成的列表示, 并且这个标量列唯一确定了 $m’ \in X’’$ 中这个元素. 同理 $\forall u = U, u = (u_1, \cdots, u_m)$ 其也唯一确定了元素 $l’ \in U’’$. 这里 $T’’ = T$ 意味着 $T’’$ 将 $(x_1, \cdots, x_n)$ 在 $X’’$ 中对应的映射映射为 $(u_1, \cdots, u_m) = T(x_1, \cdots, x_n)$ 在 $U’’$ 中对应的元素, 即 $T(x_1, \cdots, x_n) = T’‘(x_1, \cdots, x_n)$.
$((T’)’ f(x), l) = (f(x), lT’) = (m’, m) = (m, x)$, 别忘了这里 $m’, x$ 具有相同的 n 元标量列表示. $(m, x) = (T’l, x) = (l, Tx) = (l, u) = (l’, l)$. 这里 $l’ = (gT)(x)$. 即 $((T’)’ f(x), l) = ((gT)(x), l), \forall l, \forall x$ 成立. 即映射 $T’’ \circ f = g \circ T$. 这里 $f(x_1, \cdots, x_n) = (x_1, \cdots, x_n), g(u_1, \cdots, u_m) = (u_1, \cdots, u_m)$. 对于任一 $(x_1, \cdots, x_n), T’’ f(x_1, \cdots, x_n) = T’‘(x_1, \cdots, x_n), gT(x_1, \cdots, x_n) = T(x_1, \cdots, x_n)$.
定理 5, 定理证明倒是不难, 主要是搞清楚定理讲的什么. 还是得画个图:
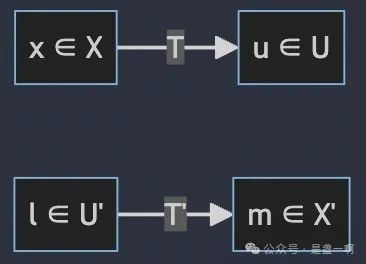
$R_T^{\perp} = { l \in U’ \mid \forall u \in R_T, l(u) = 0 }, N_{T’} = { l \in U’ \mid T’(l) = 0, \forall x \in X, T’(l)(x) = 0 }$. 从这俩集合定义来看易证 $R_T^{\perp} = N_{T’}$.
定理 5’, 关于这里 $R_T = N_T^{\perp}$ 我们已经解释过其并不是传统意义上的同一个集合.
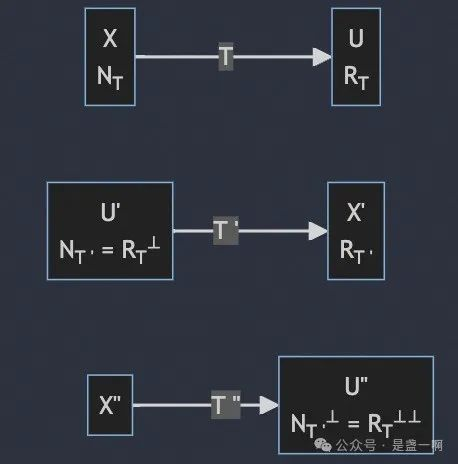
定理 6, 定理 6’; 参考上图也更清晰一点.
$\mathcal{L}(X,X)$ 是环, 并不是交换环, 也更不是整环. Lax 老师喜欢把环叫做代数, 比如后面也有个 “交换的子代数” 就是交换子环.
练习 9 证明: 由 $B(x) = 0$ 推出 $A(B(x)) = A(0) = 0 = (AB)(x) = I(x) = x$. 即 $B(x) = 0$ 当且仅当 x = 0. 则易证 B 是单射, 反证 $\exists x_1 \ne x_2, B(x_1 - x_2) = 0, x_1 = x_2$ 矛盾了. 由定理 2 推论 B 得知 B 是满射. 即 B 可逆. $AB = I, ABB^{-1} = B^{-1}, A = B^{-1}$.