系列导言, 本文是作者在学习 Peter D. Lax 线性代数及其应用的读书笔记, 侧重于记录我当时没有看懂的部分, 以及对书中部分知识点的一些扩展. 非常零散, 不成系统. 对本系列的使用最好是读者也在学习 Peter D. Lax 线代并且恰好有某处不太明白, 可以参考着本系列说不定这里就有答案. 本系列文章在写作时参考了互联网上零零散散非常多的资料在此表示感谢!
定理 2, 略作补充. 定义 $S: X/N_T \to R_T; S([x]) = T(x)$, 则易证 S 是线性映射且 S 是满射. 所以 $X/N_T, R_T$ 同构. 定理 2 表明了, 若 $\dim X \lt \dim U$ 则 $\dim R_T \lt \dim U$, T 不可能是满射. 同理若 $\dim X \gt \dim U$, 则 T 不可能是单射. 即当 $\dim X \ne \dim U$ 时 T 不可能是双射, 怪不得 mn 矩阵不可能是可逆的==
推论 B, 这里易证 T 是单射且满射.
练习 2 证明: 定义一个映射 $T: R^n \to R^m, T(x_1, \cdots, x_n) = (u_1, \cdots, u_m), u_i = \sum_{j=1}^n t_{ij} x_j$. 易证 T 是一个线性映射. 且 $\forall x \ne 0, T(x) \ne 0$, 假设 $\exists x_1 \ne 0, T(x_1) = 0$, 由原文可得 $T(x) = u = (u_1, \cdots, u_m)$ 有唯一解 $x_0, T(x_0) = u, T(x_0 + x_1) = T(x_0) + T(x_1) = T(x_0) = u$ 矛盾了.
移除第 i 个方程之后得到新的方程组, 易证这里 $x_0$ 仍是方程组的解, 假设此时方程组还存在其他解 $x_1$, 令 $k_i = x_1 - x_0, k_i \ne 0$, 易证 $T(k_i) = (0, \cdots, 0, u_i, 0 \cdots, 0), u_i \ne 0$. 若 $i = 1, \cdots, m$ 时本假设仍然成立则可知 $\exists k_i, i\in [1,m]$, 易证 $T(k_i)$ 是 $R^m$ 基, 此时 $\forall y \in R^m, y = \sum_j a_j T(k_j), x = \sum_j a_j k_j \in R^n, T(x) = y$, 即 T 是满射 $R_T = R^m$. 由定理 2 可知 $\dim R_T \le \dim R^n \lt \dim R^m$ 矛盾了. 所以在 $i = 1, \cdots, m$ 中至少有一个 o, 当移除第 o 个元素之后方程组仍能保持唯一解.
依此类推可得结论, 此时移除第 o 个方程之后方程组仍然只有唯一解, 重新从头开始再次论证即可.
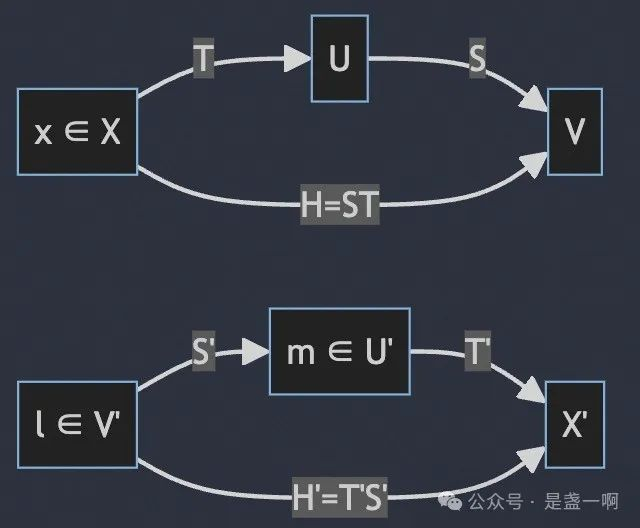
转置, 对于线性映射 $T: X \to U$, 可以定义映射 $h: U’ \to X’, h(l) = lT$, 易证这里 $lT \in X’$ 且 h 是 $U’ \to X’$ 的线性映射, 定义 h 为 T 的转置, 用 $T’$ 标识 $T’l = lT, (T’l, x) = (l, Tx) = (lT)(x)$.
P.S. 这里介绍了矩阵的若干运算所具有的语义, 我总算知道转置的实际意义是啥了…
$(ST)’ = T’S’$ 证明: 设 $H = ST, (H’l, x) = (l, Hx) = (lH)(x) = (lST)(x) = (lS)(Tx)$, 这里 $lS = S’(l), (lST)(x) = (S’(l))(T(x))$. 令 $m = S’(l), m(Tx) = (m, Tx) = (T’m, x) = (T’S’l, x)$. 即 $\forall x, (H’l)(x) = (T’S’l)(x)$, 所以映射 $H’l = T’S’l$, 别忘了陶哲轩 analysis 定义过映射相同的概念. 考虑到 $\forall l, H’l = T’S’l$, 所以映射 H’ = T’S’. 结合下面图看可能会更清晰.
$(T^{-1})’ = (T’)^{-1}$ 证明, 结合着图看可能更清晰一点.
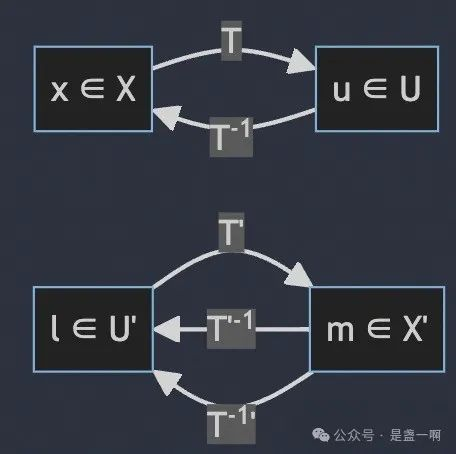
首先证明 T’ 是线性同构. $\forall l_1, l_2 \in U’, T’(l_1) = T’(l_2), l_1T = l_2 T$, 即 $(l_1 - l_2)T = 0$, 这里 0 代指 $Z: X \to K, \forall x \in X, Z(x) = 0$ . 令 $l’ = l_1 - l_2, \forall x \in X, (l’T)(x) = l’(T(x)) = 0$ 这里 T 是线性同构, $T(X) = U$, 即 $\forall u\in U, l’(u) = 0, l_1 = l_2, T’$ 是单射. 现在证 $T’$ 是满射, $\forall m \in X’, l’ = mT^{-1}, l’: U \to K$, 易证 $l’ \in U’$. 易证 $T’(l’) = m$.
欲证映射 $(T^{-1}) ‘ = (T’)^{-1}$, 即证 $\forall m \in X’, (T’)^{-1}(m) = (T^{-1}) ‘(m)$, 即证 $\forall u \in U, (T’)^{-1}(m)(u) = (T^{-1}) ‘(m)(u)$. 设 $l = (T’)^{-1}(m), T’(l) = m; T^{-1}(u) = x, T(x) = u$. 则 $(T^{-1}) ‘(m)(u) = ((T^{-1}) ‘(m), u) = m (T^{-1} (u)) = (m, x) . (T’)^{-1}(m)(u) = (l, u)$. 即证 $(l, u) = (m, x)$. 由 $(m, x) = (T’l, x) = (l, Tx) = (l, u)$ 可证…
$I’ = I$ 证明. $T T^{-1} = I, I’ = (T^{-1})’ T’ = I$.
例 10, 这里重新组织下. 已知 $(l, u) = \sum_{i=1}^m l_i (\sum_{j=1}^n t_{ij} x_j) = \sum_{j=1}^n (\sum_{i=1}^m l_i t_{ij}) x_j$. 观察到 $\sum_{i=1}^m l_i t_{ij}$ 定义了个 $U’ \to X’$ 的映射 $T_1$, 易证 $T_1$ 是线性映射. 接下来证 $T_1 = T’$, 即证 $\forall l,x, T’(l)(x) = T_1(l)(x)$. 这里 $T’(l)(x) = (l, Tx) = \sum_{i=1}^m l_i (\sum_{j=1}^n t_{ij} x_j)$. 同时 $T_1(l)(x) = \sum_{j=1}^n (\sum_{i=1}^m l_i t_{ij}) x_j$. 即 $T’(l)(x) = T_1(l)(x)$.
P.S. 这里换成矩阵的写法, 怪不得矩阵的转置是行列互换.
\[Tx = \begin{pmatrix} t_{11} & t_{12} & \cdots & t_{1n} \\ t_{21} & t_{22} & \cdots & t_{2n} \\ \vdots & \vdots & \cdots & \vdots \\ t_{m1} & t_{m2} & \cdots & t_{mn} \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix}\] \[T'l = \begin{pmatrix} t_{11} & t_{21} & \cdots & t_{m1} \\ t_{12} & t_{22} & \cdots & t_{m2} \\ \vdots & \vdots & \cdots & \vdots \\ t_{1n} & t_{2n} & \cdots & t_{mn} \end{pmatrix} \begin{pmatrix} l_1 \\ l_2 \\ \vdots \\ l_m \end{pmatrix}\]