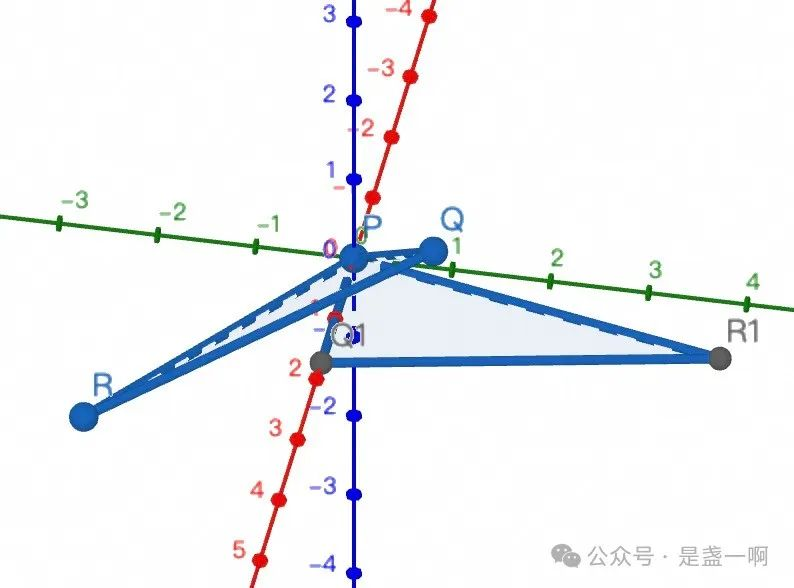
2.4.zy6, STATEMENT 1. For any three points $p, q, r \in C_n, n \gt 1$ there exists an isometry f of space $C_n$ onto itself such that
\[p'=f(p) = (0, \cdots, 0), q'=f(q) = (a_1, 0, \cdots, 0), r'=f(r) = (b_1, b_2, 0, \cdots, 0)\]where $a_1 \ge 0$ and $b_2 \ge 0$
证明: 由 f 保距性这里可以可得 $a_1^2 = a^2, (b_1 - a_1)^2 + b_2^2 = b^2, b_1 ^ 2 + b_2 ^ 2 = c^2$. 这里 $a = \vert pq\vert , b = \vert qr\vert , c = \vert rp\vert $. 易解得:
\[\begin{align} & a_1 = a \\ & b_1 = \frac{a^2 + c^2 - b^2}{2a}\\ & b_2 = \frac{\sqrt{(a+b+c)(a+c-b)(a+b-c)(b+c-a)}}{2a} \end{align}\]这里 a, b, c 为三角形三边, 易得 $a+c - b \gt 0, a + b -c \gt 0, b+c-a\gt 0$, 所以 $b_2$ 解存在.
现在我们只考虑 n = 3 的情况, 并假设 p,q,r 三点不共线情况. 若 p,q,r 三点共线, 话说这里我们尚未定义过共线, 这里将点 r,p,q 共线定义为 $\exists x, r = p + x(q-p)$, 则我们总可以捏造出一个不在该线上的 s, 比如 $s = (\frac{p_1 + q_1}{2}, \frac{p_2 + q_2}{2} + 1, \frac{p_3 + q_3}{2})$ 然后考虑 p, q, s.
此时知 $\vec u=\overrightarrow{pq}, \vec v=\overrightarrow{pr}, \vec w=\overrightarrow{pq} \times \overrightarrow{pr}$ 两两正交构成一个基是一个基还是一组基?. 同理 $\vec{u’}=\overrightarrow{p’q’}, \vec{v’}=\overrightarrow{p’r’}, \vec{w’}=\overrightarrow{p’q’} \times \overrightarrow{p’r’}$ 也正交并是基. $\forall x \in C_3, \overrightarrow{px} = \lambda_1 \vec u + \lambda_2 \vec v + \lambda_3 \vec w$, 据此定义映射 $f, x’=f(x), [x’-p’] = \lambda_1 \vec{u’} + \lambda_2 \vec{v’} + \lambda_3 \vec{w’}$, 易证 f 是等距映射且满足题目中要求.
P.S. 可以参见 2.4.1.ggb, 滑动 p,q,r 三点了解对应的映射如何变换.
We refer to the subsets of space $C_n$, which are isometric with space $C_1$, as Cartesian lines or briefly lines. A special case of the Cartesian line is the set of points of the form $x=(x_1, 0, \cdots, 0)$. This line will be denoted by $C_{n,1}, n \gt 1$.
由 2.4.zy6 可知, 当 r 在 pq 直线上时, 此时 $b + c = a, b_2 = 0$. 可以试着调动 2.4.1.ggb 中的点使其共线, 如下:
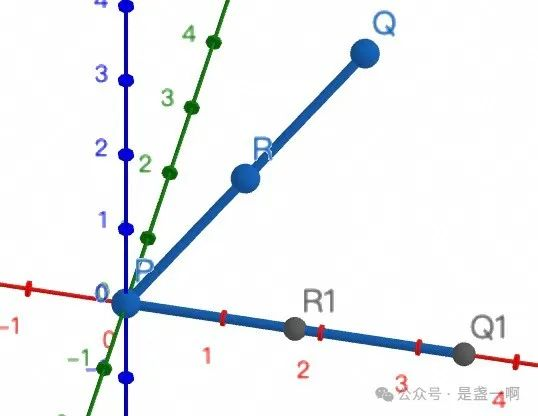
因此可以定义映射 $g: L \to C_1, g(p) = (0), g(q)=(a_1), g(r)=(b_1)$, 易证 g 双射且等距, 即给定不同的两点 $p, q, C_3$ 中一个子集 $L={p+t(q-p) \mid t\in \mathbb{R}}$ 与 $C_1$ 是 isometric metric space. 这个子集 L 就是直线.
2.4.zy7, For any point a and any vector $\vec a \ne 0$ in space $C_2$ there exists just one line L passing through point a and perpendicular to vector $\vec a$.
证明: 过 a 点做与 $\vec a$ 平行的直线 L, 假设存在直线 $L_1 \perp L, L_2 \perp L$. 由 FOGB STATEMENT 4 可知此时存在等距映射 $f(L) = C_{2, 1}, L_1’=f(L_1), L_2’=f(L_2)$. 考虑到等距映射保持内积不变可得 $L_1’ \perp C_{2,1}, L_2’ \perp C_{2,1}$. 令 $\vec w=[w_1, w_2], \vec u=[u_1,u_2], \vec v=[0, v_2]$ 分别是与 $L_1’, L_2’, C_{2,1}$平行的向量, 此时 $\vec w \perp \vec v, \vec w \cdot \vec v = 0 = \vec u \cdot \vec v, w_2 = u_2 = 0$, 即 $L_1’ = L_2’$.
P.S. 这个证明只是想展示下原文所说: Because of STATEMENT 4, to establish a property of the line in space $C_n$ (external property, i.e. property relating the line to the entire space $C_n$ as well) it is sufficient to prove it for the line $C_{n,1}$.
2.4.zy8, 直线 $L_1: \alpha_0 + \alpha_1 x_1 + \alpha_2 x_2 = 0, L_2: \beta_0 + \beta_1 x_1 + \beta_2 x_2 = 0$ 是同一条直线当且仅当 $\exists \lambda \ne 0, (\alpha_0, \alpha_1, \alpha_2) = \lambda (\beta_0, \beta_1, \beta_2)$ 成立.
证明: 当 $L_1, L_2$ 是相等直线, 意味着集合 $L_1 \subseteq L_2, L_2 \subseteq L_1. \forall (x_1, x_2) \in L_1$. 此时 $x_1 = \frac{-\alpha_2 x_2 - \alpha_0}{\alpha_1}, (x_1, x_2) \in L_2$, 即 $\frac{\beta_2 \alpha_1 - \beta_1 \alpha_2}{\alpha_1} x_2 = \frac{\alpha_0 \beta_1 - \alpha_1 \beta_0}{\alpha_1}$ 对任一 $x_2$ 成立. 即 $\beta_2 \alpha_1 - \beta_1 \alpha_2 = \alpha_0 \beta_1 - \alpha_1 \beta_0 = 0$, 可得结论. 令当 $\alpha_1 = 0$ 时同样易证.
Subsets of space $C_n$ isometric with space $C_2$ will be called Cartesian planes or briefly planes. A special case of the Cartesian plane is thus the set of points of the form $x={x_1, x_2, 0, \cdots, 0}$. We shall denote this plane by $C_{n,2}, n \gt 2$.
考虑不共线的 3 点 p, q, r 对应子集 $P={p + t(q-p) + s(r-p) \mid r,s \in \mathbb{R}}$ 其内每一个点都可以看作线性组合: $\vec{ps}=t \vec{pq} + s \vec{pr}$. 经过 2.4.zy6, STATEMENT 1 中等距映射 $f(s) = (x_1, x_2, 0)$. 依此构造映射 $g: P \to C_2, g(s) = (x_1, x_2)$, 易证 g 双射等距, 即子集 P 与 $C_2$ 是 isometric space.
这里易证平面 pqr 中任一直线 L 对应的点集经过 f 映射之后也是直线: 在 L 上任取 2 点 A, B, 经 f 映射之后对应 A1, B1; 则对于 L 上任一点 C, 经过 f 映射之后是 C1, 由 $\vert AC\vert = \vert A_1C_1\vert , \vert AB\vert = \vert A_1 B_1\vert , \vert BC\vert = \vert B_1 C_1\vert $ 易证 C1 在 A1, B1 确定直线上.
2.4.zy9, 平面 $P_1: \alpha_0 + \alpha_1 x_1 + \alpha_2 x_2 + \alpha_3 x_3 = 0, P_2: \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3 = 0$ 是同一平面当且仅当 $\exists \lambda \ne 0, (\alpha_0, \alpha_1, \alpha_2, \alpha_3) = \lambda (\beta_0, \beta_1, \beta_2, \beta_3)$ 成立.
证明: 当 $P_1, P_2$ 是同一平面, 意味着集合 $P_1 \subseteq P_2, \forall (x_1, x_2, x_3) \in P_1$ 有 $\alpha_1 x_1 = -\alpha_0 - \alpha_2 x_2 - \alpha_3 x_3$, 即 $\alpha_1 \beta_0 + \beta_1 \alpha_1 x_1 + \alpha_1 \beta_2 x_2 + \alpha_1 \beta_3 x_3 = 0 = (\alpha_1 \beta_0 - \alpha_0 \beta_1) + (\alpha_1 \beta_2 - \alpha_2 \beta_1) x_2 + (\alpha_1 \beta_3 - \alpha_3 \beta_1) x_3$ 对于 $\forall x_2, x_3$ 都成立. 这意味着 $\alpha_1 \beta_0 - \alpha_0 \beta_1 = \alpha_1 \beta_2 - \alpha_2 \beta_1 = \alpha_1 \beta_3 - \alpha_3 \beta_1 = 0$. 反证: 这里仅考虑下 $\alpha_1 \beta_0 - \alpha_0 \beta_1, \alpha_1 \beta_2 - \alpha_2 \beta_1, \alpha_1 \beta_3 - \alpha_3 \beta_1$ 都不为 0 的情况, 易证此时我们总能找到 $(x_1, x_2, x_3) \in P_1, \notin P_2$.
2.4.zy10, 任一平面 P 都可以写成 $\alpha_0 + \alpha_1 x_1 + \alpha_2 x_2 + \alpha_3 x_3 = 0$ 的形式, 这里 $\vec \alpha=[\alpha_1, \alpha_2, \alpha_3]$ 被称为是 P 的法向量.
证明: 考虑平面 $C_{3,2}: x_3 = 0$, 此时其对应 $\alpha_0 = \alpha_1 = \alpha_2 = 0, \alpha_3 = 1$, 即其法向量为 $[0, 0, 1]$. 已知任一平面 P 都可以在某种等距映射 f 下对应到 $C_{3,2}, o = f^{-1}(0,0,0), q=f^{-1}(0,0,1)$, 根据 f 保持内积不变的特性易证 $\overrightarrow{oq}$ 是平面 P 的法向量.
2.4.zy14 接着 2.4.zy10 这里任选 P 中不共线 3 点 A, B, C; 则对于平面 P 中任一 D 其满足 $\overrightarrow{AD} = a\overrightarrow{AB} + b\overrightarrow{AC}$.
证明: 记 $\vec u = \overrightarrow{AB}, \vec v = \overrightarrow{AC}, \vec w = \overrightarrow{AD}$, 由 2.4.zy2 类似可证 $\vec u, \vec v, \vec \alpha$ 是基. $\vec w = r \vec u + s \vec v + t \alpha, \vec w \cdot \vec \alpha = 0$ 可得 t = 0. 题目得证.
2.4.zy11, 设不同平面 $P: C_{3,2} z=0, Q: d + ax + by + cz = 0$. 则 P, Q 具有交点当且仅当 a, b 不全为 0.
证明: 由于 P, Q 有交点 $(x_0, y_0, z_0)$ 则意味着 $d + a x_0 + b y_0 = 0$, 若 a, b 全为 0, 则意味着 d = 0, 此时由 2.4.zy9 知 P, Q 是同一平面, 矛盾了!
若 a, b 不全为 0, 则易证方程组 $z = 0, d + ax + by + cz = 0$ 有解, 即平面 P, Q 有交点.
2.4.zy12, 不同平面 $P: d + ax + by + cz = 0, Q: w + rx + sy + tz = 0$ 没有交点当且仅当 $\exists u, [a, b, c] = u[r, s, t]$.
证明: 已知存在等距映射 f 可将 P 映射到 $P’: C_{3,2}, z = 0$, 对于 Q 上任选 3 点不共线 A, B, C 经过 f 映射为 A’, B’, C’; 由 f 保距易证 A’, B’, C’ 也不共线. 对于 Q 上任一点 D, 由 2.4.zy14 已知 $\overrightarrow{AD}$ 可以表示为 $\overrightarrow{AB}, \overrightarrow{AC}$ 线性组合, 且易证 $D’=f(D)$ 也满足 $\overrightarrow{A’D’}$ 为 $\overrightarrow{A’B’}, \overrightarrow{A’C’}$ 线性组合, 即经过 f 映射之后, Q 对应着平面 $Q’: w’ + r’x + s’y + t’z = 0$. 同理 $[a, b, c] \to [0, 0, 1]; [r, s, t] \to [r’, s’, t’]$, 再由 f 保持内积不变可知 $[a, b, c] \cdot [r, s, t] = [0, 0, 1] \cdot [r’, s’, t’]$. 且易证 P, Q 有交点当且仅当 P’, Q’ 有交点, 再由 2.4.zy11 可得结论.
P.S. 当 P, Q 有交点 (A,B,C) 意味着 $[bt - cs, cr - at, as - br] \ne \vec 0$, 易证直线 $L: (A,B,C) + t[bt - cs, cr - at, as - br] \mid t \in \mathbb{R}$ 位于 P, Q 上.