右手系, 这里的 “依次序替换为” 是指从 $\vec{e_x}$ 的正向看向原点 $\vec{e_y}$ 逆时针旋转 $\frac{\pi}{2}$ 到 $\vec{e_z}$. 这里借用 3D计算器 看非常直观.
2.3.3.zy1, 设想现在有向量 $\vec u = \overrightarrow{OU}, \vec v = \overrightarrow{OV}, \vec w=\overrightarrow{OW}$, 通过平移将她们移到相同起点处. 在 OVW 确定的平面 ovw 上, 自 V 点做 OW 的垂线, 交点记为 E, 则 $\overrightarrow{OV} = \overrightarrow{OE} + \overrightarrow{EV}$, 这里 $\overrightarrow{OE}, \overrightarrow{EV}$ 分别记为 $\vec{v_x}, \vec{v_y}$. $\overrightarrow{OU}$ 做同样处理, $\vec u = \overrightarrow{OU} = \vec{u_x} + \vec{u_y}$. 同样对 $\vec s = \vec u + \vec v$ 做同样处理 $\vec s = \vec{s_x} + \vec{s_y}$. 求证 $\vec{s_x} = \vec{v_x} + \vec{u_x}, \vec{s_y} = \vec{v_y} + \vec{u_y}$. 对应图示见 2.2.2.ggb.
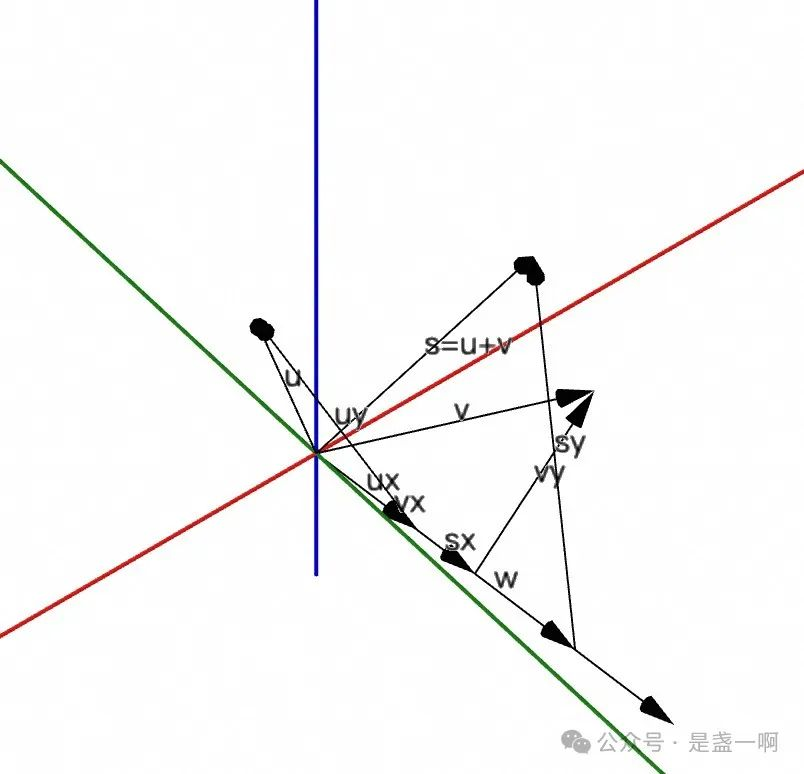
证明: 已知 $\vec s \cdot \vec w = \vec u \cdot \vec w + \vec v \cdot \vec w$. 且 $\vec u \cdot \vec w = \vec{u_x} \cdot \vec w + \vec{u_y} \cdot \vec w$, 这里 $\vec{u_y} \perp \vec w, \vec{u_y} \cdot \vec w = 0$. 可得 $\vec{s_x} \cdot \vec w = \vec{u_x} \cdot \vec w + \vec{v_x} \cdot \vec w$, 这里 $\vec{s_x}, \vec{u_x}, \vec{v_x}$ 与 $\vec w$ 在同一方向, 所以可以分别写为 $\vec{s_x} = a \vec w, \vec{u_x} = b \vec w, \vec{v_x} = c \vec w$, 即可得 $a = b + c$, 所以 $\vec{s_x} = \vec{u_x} + \vec{v_x}$. 从而可得 $\vec{s_y} = \vec{u_y} + \vec{v_y}$.
2.3.3.zy2, 接着 2.3.3.zy1, 证明 $\vec u \times \vec w = \vec{u_y} \times \vec w$.
证明: 根据外积定义已知 $\vert \vec u \times \vec w\vert = \vert \vec u\vert \vert \vec w\vert \sin(\alpha)$, 这里 $\alpha$ 为 $\vec u, \vec w$ 夹角, 有 $\vert \vec u\vert \sin(\alpha) = \vert \vec{u_y}\vert $, 即 $\vert \vec u \times \vec w\vert = \vert \vec{u_y} \times \vec w\vert $. 之后再由外积定义易得 $\vec u \times \vec w, \vec{u_y} \times \vec w$ 方向一致. 所以结论成立.
P.S. geogebra 为啥用 ⊗ 来表示外积, 每次输入都靠复制.
定理 2.3.6 $(\vec u + \vec v) \times \vec w = \vec u \times \vec w + \vec v \times \vec w$
证明: 接着使用 2.3.3.zy1 的符号, 我们只要证 $\vec{s_y} \times \vec w = \vec{u_y} \times \vec w + \vec{v_y} \times \vec w$ 即可. 这里 $\vec{s_y}, \vec{u_y}, \vec{v_y}$ 均垂直于 $\vec w$, 所以可以将她们平移到过 $\vec w$ 起点 O 的垂直平面 q 上. 见 2.2.3.ggb
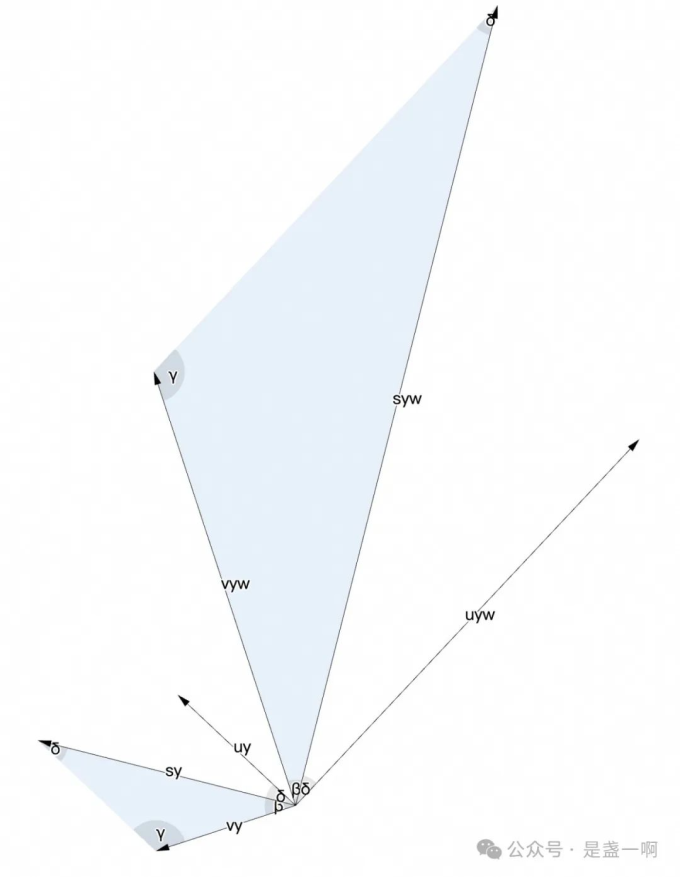
令 $\vec{uyw} = \vec{uy} \times \vec w, \vec{uyw} \perp \vec w$, 即也可以将 $\vec{uyw}$ 平移到平面 q 上, 即 $\vec{vyw} = \vec{vy} \times \vec w, \vec{syw} = \vec{sy} \times \vec w$ 都位于平面 q 上. 且 $\vec{vyw} \perp \vec{vy}, \vec{uyw} \perp \vec{uy}, \vec{syw} \perp \vec{sy}. \frac{\vert \vec{syw}\vert }{\vert \vec{sy}\vert } = \frac{\vert \vec{vyw}\vert }{\vert \vec{vy}\vert }=\frac{\vert \vec{uyw}\vert }{\vert \vec{uy}\vert }=\vert w\vert $.
如图所示, 易证图中具有相同字符的角度都是相等的, 关于这个问题我有个绝妙的证法, 可惜现在已经 23:26 了, 我得睡觉了. 所以 vyw, syw 向量终点连线与 uyw 平行, 即 $\vec{syw} = \vec{uyw} + \vec{vyw}$.
体积 = $\vert \vec u \times \vec v\vert \cdot \vert \vec w\vert \cdot \vert cos(\theta)\vert $, 见余弦定理可得原文中结论.
P.S. 图 2.9 丝毫没有看出 $\vec u \times \vec v \perp \vec u$ 的可能性..