几何学基础是我目前重建数学知识体系学习计划的一部分, 也是目前遇到自学起来较吃力的了, 主要是离公理太近了, 参考资料就很少, 我这里参考的两本书一本是 1930 年一本是 1960 年的! 毕竟现在很少有人再关心为啥平面内过一点做直线L的垂线, 垂线只有一条这种非常大众化的知识了… 我这里采用的教材是王作勤几何学基础讲义, 在我看来这本书除了部分细节缺失之外是本很好的教材, 让我对几何有了个基本的认知, 由于时间比较紧张, 我这里只学习了目前需要的前 2 章, 后续有时间的话再看看剩下的几章内容!
我一开始意味这俩是重复的:
(I.1) 对于两点 A 和 B,恒有一直线 a,它同 A 和 B 相关联。 (I.2) 对于两点 A 和 B,至多有一直线,它同 A 和 B 相关联。
这俩等价描述是:
公理 I.1(存在性公理):对任意两点 A 和 B,存在至少一条直线 a,使得 A 和 B 都在直线 a 上.
公理 I.2(唯一性公理):对任意两点 A 和 B,存在至多一条直线 a,使得 A 和 B 都在直线 a 上。
这样看是不是就觉得不重复了.. 同理 III.1 公理中 “恒有一点 B’” 等价描述是至少有一点 B’.
1.2.8.zy1, Two distinct lines can have at most one point in common.
证明: 假设有两个交点, 则根据 I.1, I.2 可知两点之间有且仅有 1 条直线, 与 distinct line 矛盾.
P.S. distinct/same, 在希尔伯特公理中, 直线, 点, 面都是不加定义的本源对象, 但是在涉及本源对象的三个不加定义的本源关系中却没有定义两个对象是否是同一个对象这种关系. 我这条命题是摘自 Hilbert’s Axioms - IME-USP, 看起来挺正规的一篇文章, 即然这篇文章这么直接用了 distinct, 我理解同一个对象/不是同一个对象这个也算是不加定义的本源关系了.
P.S. 这种贴近公理的命题证明最为头疼, 一方面这时手上能用的工具有限, 仅有寥寥几条公里, 所以证明过程特别考验想象力. 另外一方面可能一不小心就循环引证了.. 所以我个人认为对于一个教材来说, 这种时刻最好写明每一步证明过程, 不要跳, 不要显然易得容易观察到, 不要留作习题; 借此可以给读者一个照葫芦画瓢的机会; 就像陶哲轩 analysis i 前 2 章一样. 所以强力推荐此时参考 “希尔伯特几何基础-科学素养文库-科学元典丛书” 图书, 后记 “原文2”, 这里给出了很多证明.
定理 1.2.8. 共线三点,必有一点在中间. 这个用陶老师 analysis 序的三歧性类似方式描述更为清晰: 在同一直线的不同三点 A, B, C, 如下命题有且仅有 1 个成立:
- A 在 B, C 之间.
- B 在 A, C 之间.
- C 在 A, B 之间.
证明: 根据 II.3 可知如上命题至多有一条成立. 现在我们假设 1, 3 都不成立, 此时我们证明 2 是成立的. 这里对原文证明略作补充.
- 对 $\triangle EBC$ 和直线 AD 应用帕施公理,可知直线 AD 交线段 EC 于某点 F。
我的疑问是: 原文帕施公理仅证明了此时 AD 要么交于 CE, 要么交于 BC, 原文直接能直接认为 AD 交线段 EC 于某点 F 呢? 从 Pasch’s axiom wiki 上可以看到该条公理有个更现代化描述:
A more modern version of Pasch’s axiom — In the plane, if a line intersects one side of a triangle internally then it intersects precisely one other side internally and the third side externally, if it does not pass through a vertex of the triangle.
此时已知 D 是线段 BE 内点, 即 AD intersects BE internally. 且 A 不在线段 BC 内部, 即 AD intersects BC externally; 所以 AD intersects CE internally, 即 F 是线段 CE 内点.
- 可知点 D 是线段 AF 中的点
证明: 已知 G 是线段 AE 内点, 即 CD intersects AE internally; F 是线段 CE 内点, 根据 II.3 可知, C 一点不是线段 EF 内点, 即 CD intersects EF externally. 所以 CG intersects AF internally, 假设此时交点是 D’, 我们要证 D’ = D.
首先由条件可知直线 AD, CD 不是同一条直线. 反证: 假设是同一条直线, 即可得出 D 位于直线 AC 上, 这与已知矛盾. 已知此时 D, D’ 都是直线 AD, CD 交点, 则根据 1.2.8.zy1 可知 D’ = D.
定理 1.2.10, 证明见原文 2 注解 [14]. 定理 1.2.12, 证明见原文 2 注解 [13]
定义 1.2.11, 在直线 $\alpha$ 上给定任意一条直线 $\alpha$, 修正为: 在平面 $\alpha$ 上给定任意一条直线 $a$.
定理 1.2.17 略作补充
- 证明 O 不是 A 点.
证明: 反证法, 假设 O 在 A 点上, 这里 O 为 CD 与 AB 交点, D 不在直线 AB 上, 所以 ABD 可以组成三角形. 由定理 1.2.14 可知 $\angle CAB \gt \angle DBA$, 矛盾了.
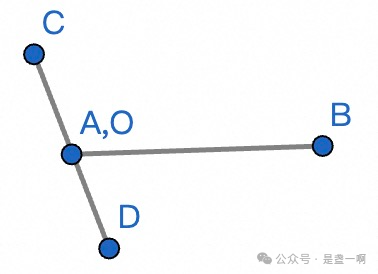
- 证明 B 不在 A 与 O 之间
证明: 反证法, 假设 B 在 AO 之间, 此时由 Pasch’s axiom 可知 DB 交 AC 于点 E.
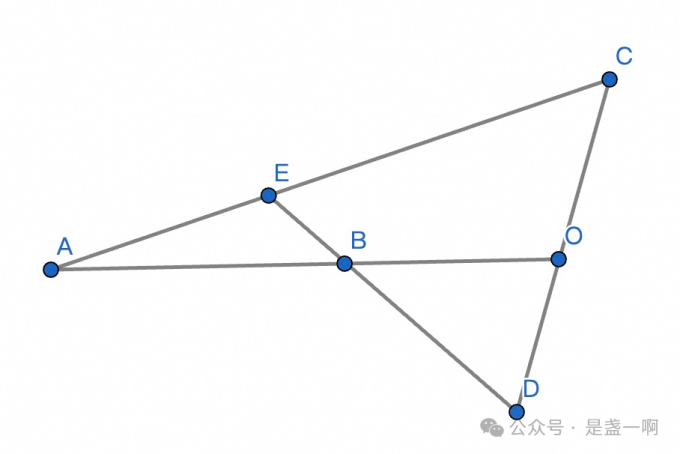
这里点 E 不在直线 AB 上, 假设 E 在 AB 上, 则直线 AE 与直线 AB 是同一个直线, 即点 C 位于直线 AB 上, 矛盾了. 所以 EAB 可以组成三角形. 由定理 1.2.14 可知 $\angle DBA \gt \angle CAB$, 矛盾了.
定理 1.2.20.
- 讨论点 A 位于直线 l 上.
证明: 首先由 1.2.19(1) 可知直角是存在的, 假设其是平面 $\alpha$ 上角 $\angle (h, k)$. 任取点 C 位于 l 之外, 则 l, C 可确定平面 $\alpha’$, 令 l 作为 III.4 公理中直线 a’, A 为点 O’, 则由 III.4 可知有且仅有 1 条射线 k’, 使得 $\angle (h’, k’) = \angle (h, k)$.
等等, 这时候在立体空间中选择不同的点 C 可得不同的平面 $\alpha’$, 即这时垂线不止一条.
- 在直线 l 的另一侧存在点 B,
解: 这里说的有点含糊了, 准确说法是 B 在直线 AE 上. 这里因为直线 AD 垂直直线 DE, 这里令 $\angle ADE$ 表示 III.4 中的 $\angle (h, k)$, 点 D 表示点 O’, 射线 DE 表示 h’, 射线 DB 表示射线 k’, 则 III.4 说明了有且仅有一条射线, 即射线 k’ 位于直线 AD 上, 即 B 位于 AD 上.
geogebra 帮助文档: 可真不好找呀. https://www.geogebra.org/m/etg2rk8j https://wiki.geogebra.org/en/Commands