前言

这里记录了在学习编译器设计这本书时记录的读书笔记, 限于每篇文章篇幅, 读书笔记被拆分成了多个部分, 这里是第一部分.

编译器书籍选择。编译原理(龙书)，编译器设计(engineering a complier)。其中编译器设计更容易上手一点，更适合实践。编译原理更偏向于理论一点，更为全面。以 dfa 最小化算法举例，编译器设计首先介绍状态等价的概念，然后介绍了算法，很直观，但是有一些方面没有涉及介绍到。比如为啥初始集合中非终结状态，终结状态不能在一起？如下面例子，根据等价的定义B,C很显然等价嘛。

而编译原理则是从状态区分概念入手介绍了最小化算法，有理有据，不过感觉不那么直观。但是呢从区分概念入手最小化算法回答了上面的问题，因为接受状态和非接受状态是可区分的，所以不能放在一个集合中。

另外, 编译器设计知识面没有编译原理涉及到的广, 还是以上面最小化算法为例. 编译原理介绍了适用于词法分析器中的最小化算法. 而编译器设计则丝毫没有提起过, 这一度让我困惑了很久. 相关细节可以往下看.

第 1 章, 编译概观

这里讲述的东西大部分已经熟知, 所以这里只介绍一些概念相关的知识点.

语法; 程序语言语法通过某种规则的有限集定义了源语言集合; 这里语法规则是有限的, 而源语言集合是无限的. 词类, syntactic category, 又叫语法范畴, 语法规则中使用词类来引用单词, 这里词类是一堆具有公共特征的单词的总称, 比如 “标识符” 词类是所有可以作为标识符的单词的总称.词素, lexeme; 可以看为是词类的一个具体实例. 词类与语法单元, 按我理解在程序设计语言语法描述中, 词类是最小的, 不可再划分的粒度; 而语法单元则可以根据语法规则进一步划分, 直至划分为词类. 词法分析器扫描输入, 生成 ‘(单词所属词类, 单词具体值)’ 流. 语法分析器扫描该流, 再根据语法来验证该流是否属于语法定义的源语言集合. microsyntax, 程序设计语言中用来描述词法结构的规则, microsyntax 定义了词类以及词类中单词的字符组合形式. 所以就能看出来了词法分析器根据 microsyntax 将字符流转换为单词流, 语法分析器根据语法验证单词流是否合法.

ILOC, intermediate language for an optimizing compiler, 可以看作某种简单的 RISC 机器的汇编语言. 参见原文了解 ILOC 语言的一些细节.

编译期指令调度, 运行时指令调度; 很显然编译期指令调度由编译器完成, 运行时指令调度由 CPU 完成. 一直以来只是知道指令调度的存在, 但却不是很清楚指令调度的具体效果; 原来举了个例子展示了通过指令调度将性能提升一倍的案例, 可以了解一下.

第 2 章, 词法分析器

2.2 识别单词

还是先了解一些概念.

状态转移图, 起始状态, 接受状态. 再来看一些状态转移图的某些约定: 接受状态以双层圆圈绘制. 通常会省去目标为错误状态的转移, 因此识别器在遇到输入字符无法匹配到状态的某个转移时, 就转移到错误状态. 状态转移图中可以存在环, 来表明到自身的转移.

FA, 有限自动机, 其定义参考原文. 转移图是 FA 的形式化表示, FA 与转移图一一对应. 另外这里可能还有一个 “接受” 的概念, FA 接受字符串 x 的充分必要条件可以参考原文了解一下.

2.3 正则表达式

还是先介绍一些概念。这里的概念最好要摸清楚, 不然后面会很迷糊吃力.

语言，单词的集合. 这里单词可以认为是词素, 语言这个概念名感觉有点违和。FA 定义的语言记为 L(F)，即 FA 接受的字符串集合。

连接, 闭包, 选择; 定义于集合之上的操作, 或者说运算符, 注意这里操作数是集合, 数学中的那个集合. 运算符具体定义参考原文了解.

正则表达式，正则表达式是一种符号表示法，描述了某个字母表 \(\sum\) 上的字符串集合，即正则表达式也定义了一个语言, 记为 L(RE), 又称为正则语言。字母表 \(\sum\) 上正则表达式集合的构造参见原文, 这里的构造方式定义了什么是正则表达式, 以及该正则表达式定义的语言(即字符串集合)是什么. 注意这里所使用的 ‘选择’, ‘闭包’, ‘连接’ 是定义在正则表达式之上的运算符, 与上面定义在集合之上的同名运算符是两回事, 虽然两者很类似. 科学论证表明，FA 与正则表达式一一对应。

正则表达式运算符; 除了上述介绍的三种基本运算符之外, 正则表达式还支持其他运算符. 正闭包, 定义见原文. 有限闭包, 定义在原文. 求补^, 这个运算符原文没有精确地介绍, 按我理解, 对于 ^R 而言, 这里要求 \(L(R)\) 的元素必须是字母表 \(\sum\) 上的字母, 即 \(L(R)\) 是 \(\sum\) 的子集, L(^R) 等于字母表 \(\sum - L(R)\). 求补~, 这个运算符原文并没有介绍就直接用了, 让我一度很困惑. 参考 wiki 百科定义, \(\sim R\) 等于 \({\sum} ^ * - L(R)\), 这里 \({\sum} ^ *\) 表示 \((a_1 | a_2 | ... | a_n) ^ *\), 其中\(\left \{ a_1, a_2,...,a_n \right \} == \sum\). 这里除了三种基本运算符之外的所有运算符都可以用三种基本运算符重写, 有限闭包, 正闭包这些显而易见, 对于求补~运算符, 按照 wiki 百科的说法也是可以重写的, 只是过程复杂了一些, 反正我是没有脑补出如何重写. 另外这里也可以看出正则表达式在三种基本运算符下是封闭的, 即将运算符应用到一个或一组正则表达式之上, 结果仍然是一个正则表达式.

正则表达式的运算符优先级; 首先 ‘()’ 仍然具有最大的优先级, 其余依次是: ‘求补^’, ‘闭包*’, ‘连接’, ‘选择’. 是的原文并没给出所有运算符的优先级, 我也没有办法.

字符范围表示, 定义参见原文, 这里为啥不用通用的 ‘[a-z]’, 而是 ‘[a…z]’ 呢?! 另外这里字符范围表示应该不能看作定义在正则表达式之上的运算符.

正则表达式 R 的补集 \(~R\) 对应的 FA; 这里记 R 对应的 FA 为 \(\left \{ S, \sum, \delta, s_0,S_A \right \}\); 则 \(~A\) 对应的 FA 为 \(\left \{ S, \sum, \delta, s_0, S-S_A \right \}\), 即交换了原来 FA 的接受状态与非接受状态.

2.4 从正则表达式到词法分析器

构造法的循环，参见原文这张图，有点意思。

2.4.1 非确定性有限自动机

老规矩, 先看一下基本概念.

NFA, 非确定性有限自动机, DFA, 确定性有限自动机; 定义参见原文. NFA 对应的状态转移图通过引入\(\epsilon\)转移来表示这种不确定性, 以原文图那个用来识别 mn 的状态转移图举例, 当处在\(s_0\)状态, 遇到 m 时, 其可以转移到\(s_1\), 也可以转移到\(s_2\). 原文也提到了两个模型, 用来描述 NFA 的行为, 以期来让 NFA 的行为更具有确定性, 这里的模型2感觉就像多重宇宙理论中所说的当遇到不确定性事, 就派生出一个新的宇宙. 根据下文可知, 原文更倾向于使用模型 2 来描述 NFA 的行为.

NFA 的配置, 就是 NFA 状态的集合; 所以具有 n 个状态的 NFA 配置最多为 \(2^n\), 即长度为 n 的集合的子集个数. 原文存在一个错误, 其认为配置总数是\({\left | \sum \right |} ^ n\), 这里也有位仁兄看出来了. NFA 验证一个字符串是否被接受的过程也就是 NFA 从一个配置跳到另一个配置的过程, 还是以原文那个用来识别 mn 的状态转移图举例, 当其用来验证输入串 “mn” 时, 其会首先从配置\(\left \{ s_0 \right \}\)跳到\(\left \{ s_1, s_2 \right \}\)最后到\(\left \{ s_3 \right \}\). 所以 NFA 接受一个字符串的充分必要条件是配置跳转路径中最后一个配置中存在至少一个终结状态. 这里还有个有效配置的概念: 即可以通过某个输入串到达的配置.

2.4.2 从正则表达式到 NFA: Thompson 构造法

Thompson 构造法大致流程: 首先为输入 RE 中每个字符构造简单的 NFA, 构造姿势参考原文; 然后按照正则表达式运算符的优先级, 将操作数对应的 NFA 按照运算符的语义转换为一个 NFA, 相当于将正则表达式运算符应用在一个或一组 NFA 上得到一个结果 NFA. 在此过程中, 始终遵循如下性质:

1. 每个构造出来的 NFA 都仅有一个起始状态, 都仅有一个接受状态; 不存在到起始状态的转移; 不存在从接受状态出发的转移.
2. each state has at most two entering and two exiting $\epsilon$$moves, and at most one entering and one exiting move on a symbol in the alphabet. 原文对这句的翻译感觉怪怪的.
3. 在连接 NFA 时, 总是使用\(\epsilon\)转移将左操作数 NFA 的接受状态与右操作数 NFA 的起始状态连接在一起.

NFA 运算, 这里介绍一下如何将一个或一组 NFA 按照正则表达式运算符的语义转换为一个结果 NFA, 由上可知, 任何正则表达式运算符都可重写为三种基本运算符: 闭包, 连接, 选择, 所以这里只会介绍这三种 NFA 运算, 如下图所示:

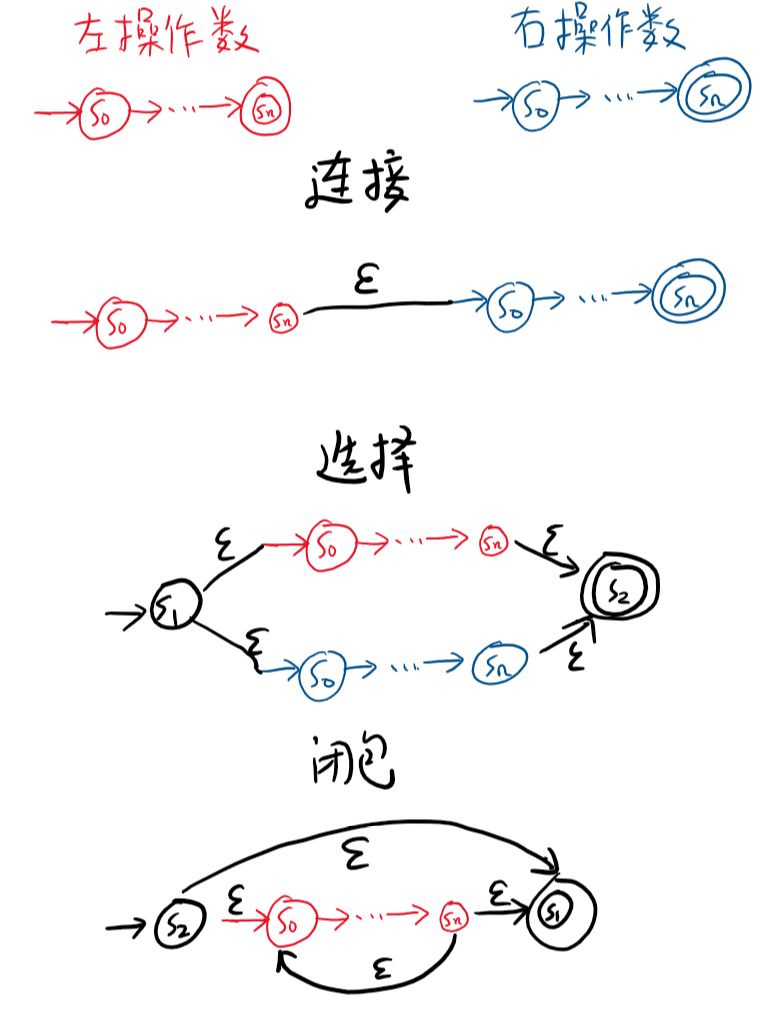
2.4.3 从 NFA 到 DFA: 子集构造法

子集构造法, 参见原文了解其输入, 输出, 以及详细过程. 没什么难点, 可能是因为并没有让我们证明这时构造出来的 DFA 与原来的 NFA 接受相同的语言. 这里可以多琢磨琢磨为何循环能被终止, 而不会发生一直循环的情况. 另外按照原文子集构造法生成的 DFA 是会存在死状态的, 关于死状态的介绍参考编译原理 3.8.4 实现向前看运算符章节中关于对死状态的介绍, 在子集构造法中消除死状态的姿势参见 re2dot.

离线计算 NFA 中每个状态的 \(\epsilon-closure\); 这个算法初看有点绕. 其主要是利用\(\epsilon-closure(s) = \left \{ s \right \} U {\bigcup}_{{s\overset{\epsilon}{\rightarrow}p}\in \delta_N} \epsilon-closure(p)\)这个递推公式来构建的. 算法中用 E(s) 存放 \(\epsilon-closure(s)\). worklist 是状态集合, 其内每一个状态 s 对应的 E(s) 等待着求解, 初始时 worklist 等于全部状态, 毕竟这时每一个状态都等待着求解 E(s). 然后对于 worklist 中每一个字符 s, 算法利用上面的递推公式根据目前 E 中保存的信息, 求解出 \(E_1(s)\); 若 \(E_1(s) == E(s)\) 则不需要更新 E. 否则使用 \(E_1(s)\) 更新 E, 同时根据递推公式这时还需要更新哪些依赖着 E(s) 的状态 d 对应的 E(d), 即会把 d 再仍回 worklist 中. 再看一下为何这里的循环能终止, 由于 E(s) 只增不减, 然后\(\epsilon-closure(s)\)又是有限集合, 所以循环总会终止的, 可以多琢磨琢磨, 能严格证明就更好了.

2.4.4 从 DFA 到最小 DFA: Hopcroft 算法

状态等价, 等价的状态对于任何输入字符都将转移到已经等价的状态中. 可以将 DFA 中等价的状态当作一个状态来处理, 如下例子:

可以看到 B, C 是等价的, 所以可以将其作为一个状态来处理即如下 DFA 所示, 可以证明这里两个 DFA 接受相同的语言. 注意这里接受状态，非接受状态一定不会是等价的，即使它们看上去很相似，参见最上面前言中介绍。

集合划分, hopcroft 中会用到这个概念, 定义参见原文.

Hopcroft 算法; 就是利用等价的概念来最小化 DFA. 之所以这里叫 “最小化”, 而不是 “小化”, 是因为大佬们已经证明了 Hopcroft 算法生成的 DFA 就是接受相同语言前提下状态最小的 DFA 了.

Split 函数，在看 hopcroft 算法之前首先看下 split 函数。其输入是DFA状态集的子集S以及DFA状态集的一个集合划分T。位于T 中相同元素的两个状态可能是等价的。位于T中不同元素的两个状态一定是不等价的。split 输出是 S 的集合划分 Sout。同属于 Sout 同一个元素的状态可能是等价的。属于 Sout 中不同元素的状态一定是不等价的。Split 函数以伪代码的形式描述如下:

// ch 是 DFA 字母表某个字母。
Split(S, T, ch) {
    // m 是个 map, 其 key 是集合，取值可能是 T 中某个元素，也可能是空集。其 value 部分也是状态集合。
    m = {}  
    for s in S { 
        if exists move(s, ch) { 
            // T.get(s) 返回 T 中某个元素，其包括了状态 s。T 中必有一个元素而且仅有一个元素包括了 s。
            k = T.get(move(s, ch))
        } else { 
            k = {}  // 空集
        }
        m[k].append(s)
    }
    // 这里返回值符合上面对 Sout 的定义。
    return m.values()
}

Split(S,T) {
    // DFA.letters，DFA 字母表。
    for ch in DFA.letters {
         S1 = Split(S,T, ch)
         if len(S1) > 1 {
             return S1
         }
    }
    return {S}  // 只有一个元素 S 的集合。
}

Hopcroft 算法实现，参见原文。其中 Split 定义见上。之后根据集合 P 来构造新 DFA。把 P 中每一个元素都视为新 DFA 的状态。若 P 中元素包括了原 DFA 的初始状态，那么该元素对应新 DFA 的状态就是初始状态。若 P 中元素包括了原 DFA 的接受状态，那么该元素对应新 DFA 的状态就是接受状态。新 DFA 转换表的构建参见原文。

Hopcroft 算法循环可终止性分析，参见原文。

适用于词法分析器的 DFA 最小化算法，注意原来这里介绍的最小化并不适合词法分析器因为该算法会丢失掉一些信息，具体细节见下。

2.5 实现词法分析器

词法分析器的功能; 之前已经介绍了, 这里再说一次. 词法分析器的输入是表示源文件的字节流, 输出是 <语法范畴, 词素> 序列.

词法分析器的不同实现姿势; 原文给出了三种实现词法分析器的方式, 每个方式的具体细节下面会介绍. 值得注意的是三种实现方式效率的差别仅在于处理每个字符的常量成本, 而扫描的渐进复杂度是相同的, 均为 O(n), 其中 n 为输入串的长度. 下面依次介绍这三种姿势的词法分析器.

表驱动词法分析器对外提供的接口; 如下所示:

struct Lexer {
    Lexer(DFA *fa, Input *in);
    Token GetToken();
};

该接口期待用户的使用姿势是: 用户首先应该初始化一个 Lexer 实例, 传递相应的信息; 如上所示需要传递一个 DFA 实例, 表明待执行的 DFA; 以及输入流 in, Lexer 通过 in 来读取用户等待词法分析的源文件. 然后用户一直调用 GetToken(), 直至 GetToken() 返回 kEOF, 每次调用 GetToken() 都会返回下一个 <语法范畴, 词素> 组合.

表驱动词法分析器 v1.0 实现; 在 v1.0 中, Lexer 初始化逻辑很简单, 就是把 fa, in 保存下来供 GetToken() 调用时使用. 下面主要介绍 GetToken() 的实现, 如下以伪代码的形式介绍:

Token GetToken() {
    state = s0  // 当前状态
    lexeme = ""
    stack.clear()  // 状态栈, 用来记录本次 GetToken() 走过的状态用来回溯.    
    // 如下是每次循环开始都成立的不变量:
    // lexeme 记录了输入流 in 中已经读取到的字符, 即 lexeme + in 中未读取的字符 = 整个输入源文件.
    // stack 栈顶状态经由 lexeme 末尾字符转移会到达 state 所指的当前状态. 
    while (true) {  // 读取, 开始~
         if (state.IsAccept()) {
             // 遇到了一个接受状态, 在回溯时回溯到这个状态就足够了. 
             // 所以此时 stack 中记录的状态都不再重要了, 扔掉她们.
             stack.clear();  
         }
         ch = in.next()  // 输入流中下一个字符.
         if (ch == kEOF || !fa.ExistMove(state, ch)) {
             // 输入结束, 或者当前状态 state 不存在针对 ch 的转移.
             break         
         }
         stack.push(state)
         lexeme.append(ch) 
         state = fa.Move(state, ch)
    }
    // 此时表明识别遇到了问题, 可能需要回溯, 记得这时上面的不变量仍然成立.
    // 这里每次循环开始, 上面的不变量仍然也成立. 
    while (!state.IsAccept() && !stack.empty()) {   // 回溯, 开始~
        state = stack.pop();
        // 根据上面的不变量, 可以由 !stack.empty() 推断出 lexeme 也不为空.
        lexeme.pop_back();
        in.Rollback();  // in 回退一个位置.
    }
    if (!state.IsAccept()) {
        // 此时输入流 in 的状态与进入本次 GetToken() 调用时一致, 
        // in 的状态主要是包括 in 内部的读写指针这些. 
        return kErrorToken 
    }
    // 根据当前 state 对应的信息构造 Token 实例, 后面会讲到此时 state 中会存放着哪些信息.
    return Token(state, lexeme);
}

可以看出这里的 GetToken() 和原文有一些细节方面不太一致, 主要是引入了几个不变量可以帮助更好的理解执行流程. 另外原文的 truncate lexeme 会在 lexeme 为空时也执行, 我觉得应该是个 bug 了, 不信可以手动跑一下.

表驱动词法分析器 v2.0 实现. 在 v1.0 中, 某些案例会导致平方级别 \(O(n^2)\) 的回滚(具体是指 in.Rollback() 这些)调用数目, 其中 n 为输入串长度. 如原文 \(ab|(ab)^*c\) 例子, 这里以原文例子图中的 DFA, 输入串 “abababab” 作为 Lexer 初始化参数构造 Lexer 实例, 然后调用 GetToken(). 此时第一次调用会读取整个输入串, 然后回溯 6 次, 返回 “ab”. 第 2 次调用也会读取完整个输入串, 然后回溯 4 次, 返回 “ab”… 更广义上讲, 假设输入串长度为 n, 那么最坏情况下, 回溯次数为 \(1 + 2 + 3 + ... + n = \frac{n * (n-1)}{2} \approx O(n^2)\), 我自己瞎想出来的, 没证明过. 所以就有了 v2.0, v2.0 大体上是空间换时间的思路, 就是在每次 GetToken() 调用的回溯阶段记录下来哪些会进入死状态的转移, 然后在后续 GetToken() 调用中读取阶段, 如果发现当前转移已被记录是会走向死状态的, 那就终止读取立即开始回溯. 所以记录转移是否会走向死状态的信息是 Lexer 实例级别的, 每次 GetToken() 都是读写这部分信息. 现在就有一个问题, 如何来表(存)示(储)”该转移会进入死状态, 禁止通行”这种信息? 原文是通过 Failed 二维数组来表示的, 数组的行对应于 DFA 的每一个状态 s, 数组列对应于输入流中的位置 off, 就像 Linux 文件抽象一样, 文件就是一个字节数组, 其内每一个字节都有一个相对于文件开始的偏移量, Failed 数组列记录的就是这个偏移量. 所以输入流有多长, 就有多少数组列. 若 Failed[s][off] 取值为 true, 则表明在状态 s 上, 读取 off 指定位置的字符并进行的转移最终会走向死状态. 话说回来关于 Failed 数组, 我一开始纳闷为啥数组列记录的是输入流偏移. 而不是字母表中的字母 c, 表明在状态 s 执行字母 c 对应的转移最终会进入死状态. 后来意识到这时是否会进入死状态还与 c 后续的字母有关, 以下面的状态转移图举例, 从状态 A 开始, 若字母 c 后面跟着个字母 d, 那么是不会进入死状态的. 反之如果后面跟着个字母 e 那就会进入死状态了.

在 v2.0 中初始化 Lexer 实例时, 除了 v1.0 的行为之外, 还需要根据 DFA 状态数以及输入流内容长度构建 Failed 二维数组, 并将其值全初始化为 false. 此时的 GetToken() 与 v1.0 版总体结构相差无异, 具体实现如下, 与 v1.0 版行为一致的地方将不再额外注释:

Token GetToken() {
    state = s0; 
    lexeme = '';
    // stack 中元素形式为 <state, off> 对应于 Failed 数组行与列. 
    stack.clear();
    pos = in.lseek();  // 获取输入流 in 当前偏移.
    // 此时的不变量除了 v1.0 中引入的之外, 还额外引入了:
    // pos 始终与 in.seek() 保持一致, 即 pos == in.seek() 总为 true.
    // stack 栈顶元素中 off 值就是 lexeme 末尾字符在输入流 in 中的偏移.
    // 根据这些不变量可以推断出:
    // pos == stack.back()[1] + 1, 即 pos 值等于 stack 栈顶元素 off 值 + 1.
    // stack 元素从栈底到栈顶, off 值始终以 1 递增.
    while (true) {
        if (state.IsAccept()) {
            stack.clear();
        }
        if (Failed[state][pos]) {
            // 在状态 state 读取 pos 处的字符并进行转移最终会进入死状态, 所以终止读取
            break ;
        }
        ch = in.next() 
        if (ch == kEOF) {
            break         
        }
        if (!fa.ExistMove(state, ch)) {
            in.Rollback();  // 为了保持 "pos == in.seek()" 这一不变量.
            break ;
        }
        stack.push(<state, pos>)
        lexeme.append(ch) 
        state = fa.Move(state, ch)
        ++pos
    }
    while (!state.IsAccept() && !stack.empty()) { 
        state, pos = stack.pop();
        Failed[state][pos] = true;  // 可以根据目前知识更新 Failed 了
        lexeme.pop_back();
    }
    // 并没有在回溯 while 循环中通过 in.Rollback() 回溯输入流, 主要是想着节省那么几次系统调用.
    // ~~在一个伪代码描述算法中, 至于整这些歪门邪道么~~.
    in.seek(pos);  
    if (!state.IsAccept()) {
        return kErrorToken 
    }
    return Token(state, lexeme);    
}    

直接编码的词法分析器, 也就是通过显式地 if…else… 或 switch…case… 也隐式表示 DFA, 具体操作姿势参见原文图2-16. 与上面的表驱动法相比, 直接编码更特化了一些. 我个人对这个没啥兴趣, 所以需要的同学可以直接去看原文.

手工编码的词法分析器; 与上面的直接编码相比, 手工编码更特化了一些, 比如在语法范畴仅表示一个词素时(就像关键词, 运算符们对应的语法范畴), 不再在 GetToken() 中返回 lexeme 部分. 而且更偏向于工程方面的优化, 比如引入输入流缓冲这些. 我个人对这个没啥兴趣, 所以需要的同学可以直接去看原文.

现实世界中的词法分析器如何编写; 因为词法分析器接受的输入是多个正则表达式, 所以词法分析器会将这些正则表达式通过选择运算符叠成一个正则表达式, 然后转换成 NFA, 这时可以做到根据 NFA 的接受状态确认此接受状态对应于输入中哪个或哪些正则; 然后利用子集构造法将 NFA 转 DFA, 这时 DFA 接受状态 x 可能对应于多个原 NFA 接受状态 y1,…,yn, 可以证明若某个输入串被 x 接受, 那么这个输入串也能被 y1,…,yn 接受. 然后最小化 DFA, 如果这时按照原文中的最小化算法, 那么当最小化 DFA 进入接受状态时, 无法根据这个状态得知当前 lexeme 究竟是被哪个正则表达式识别了, 只知道是被其中一个正则表达式识别了. 所以就不能照搬原文的最小化算法, 而且原文还很坑地没有介绍这种情况, 所幸编译原理介绍了这种情况以及如何处理. 参见编译原理 3.9.7 词法分析器的状态最小化章节. 利用这个最小化算法可以做到若最小化 DFA 接受状态对应着原 NFA 多个接受状态, 当最小化 DFA 接受了某个输入串, 可以证明对应着的多个原 NFA 接受状态同样会接受该字符串. 此时具体对应于哪个正则应该由用户来选择, 比如 lex 就遵循谁先出现选择谁.

2.6 高级主题

不感兴趣, 没深入了解, 有需要可以直接去看书~.

第 3 章 语法分析器

老规矩先来看几组概念

上下文无关语法，参见之前对语法的定义，上下文无关语法就是语法的一种。其定义的语言被称为上下文无关语言。

成员资格判定，即判定给定的句子是否属于给定语法定义的语言。若此时句子S属于语法G定义的语言，可以说G能推导出S。

程序设计语言，一般都是上下文无关语法来描述。当然可以使用非上下文无关语法来描述了但是这样做的话可能就找不到足够高效的算法来进行成员判定。

语法分析器，给定语法G以及输入句子s，语法分析器会判断s是否是G定义的语言，若不是则报错。反之则将句子s各个组成部分适配到G的语法模型中，即找到G生成s的一个推导。这整个过程则称为语法分析。

3.2 语法的表示

为啥不用正则表达式，参见原文了解，主要就是正则表达式无法计数，不能用来表示成对结构，而成对结构在程序设计语言中被大量使用。

上下文无关语法严格定义，通过四元组(T,NT,S,P)来指定一个上下文无关语法。参见原文对该四元组的定义。

BNF 上下文无关语法的传统符号表示，参见原文了解。

推导，句型，推导一步或多步，这些概念定义参见原文。根据原文定义句型可以是完整句子。

语法分析树，用来表示推导过程的树，语法分析树只能展示使用了哪些规则，并不能展示应用这些规则的顺序。

二义形语法，对于语法G而言，如果存在一个句子s，使得G到s存在多种推导，那么G就称为二义形语法。这里存在多种推导意味着存在多棵语法树. 语法 G 是否是二义性是不可判定的, 即不能在有限步骤内判断一个给定的语法是否是二义的.

最左推导，最右推导，按我理解最左/最右推导是指在自顶向下语法分析的过程中每一步都对第一个尚未尝试过的最左/最右非终结符应用其对应产生式。

程序设计语言的部分语义可以直接编码到其语法中，参见原文例子。在原文中，表达式的第一个上下文无关语法描述没有完全将运算符优先级这种语义范畴的信息编码到语法中，”没有完全”是指该语法仅把括号为最高优先级这一语义事实编码到语法中。导致根据该语法推导生成的语法分析树对表达式求值时，无法采用后序遍历这种常规遍历来遍历语法树。原文随之又给出了另一种对表达式的语法描述，该语法通过引入额外的产生式将优先级信息编码到语法中了，基于该语法推导生成的语法分析树通过后序遍历即可正确地完成对表达式的求值。

上下文无关语法的层次，上下文无关语法按照每个语法对应语法分析的运行效率(时间复杂度)分为了多个层次，运行效率从低到高排序: 上下文无关语法，\(O(n^3)\)，这么说所有的上下文无关语法都是可进行语法分析的啊; LR(1)，\(O(n)\)，可从左到右扫描输入，自底向上进行语法分析; LL(1)，\(O(n)\)，可从左到右扫描输入，自顶向下进行语法分析; RE 正则表达式，\(O(n)\)，可利用 DFA 进行语法分析。其中 n 为输入流中终结符的数目，对于正则表达式，字母就是终结符。语法分析运行效率越高，表达能力就越受限，比如就像之前讲的正则表达式无法计数无法表示成对结构。而LL(1)就成。但树上没提给定一个语法如何判定其所属层次啊。

语法分析的自顶向下，自底向上。首先明确一下语法分析的输出就是语法分析树，毕竟语法分析是找推导的过程，而推导可用语法分析树来表示。然后参见原文对这两个概念的定义，

3.3 自顶向下语法分析

最左匹配的自顶向下语法分析器算法，参见原文，这里并不考虑存在\(\epsilon\)产生式的情况，毕竟在不考虑接受空串的语法中，我们总可以消除掉\(\epsilon\)产生式。这里每次循环开始都成立的不变量有，focus 始终指向当前语法分析树的叶子结点，接下来的循环将会检测或进一步展开 focus。stack 栈顶元素是 focus 后继。从而可以得出 stack 中位于底部的元素始终是位于顶部元素的后继。另外注意在回溯时一方面要确保上述不变量始终成立。另外一方面也要注意对输入流的回溯，一个简单的方法就是将回溯过程中遇到的终结符号再依次压入输入中。产生式的选择，对于一个非终结符节点来说，算法会将已经使用过的产生式记录在节点中，然后再下一次选择时选择一个未使用的产生式。

根据算法过程可以看出，算法仅在遇到一个非终结符节点时，才会消耗输入流。在决策如何选择产生式的时候是依据产生式在语法描述中的次序，并未依赖输入流中的信息。所以本章后面章节的”前瞻一位符号”的意思是指会根据输入流中下一个符号来决策选择哪个产生式。我本来以为的前瞻是指除了原文算法中那个已经读取出来的 word 之外再读取一个符号，然后依据这2个符号的信息来决策如何产生式来着。

3.3.1 为进行自顶向下语法分析而转换语法

左递归，定义参见原文。其中间接左递归规则按我理解是指规则右侧第一个符号经过一次或多次推导能推导出以规则左侧符号开头的符号串。原文只是说经过一次或多次能推导出来左侧符号，并未明确约束左侧符号要在第一位。

直接左递归的消除，原文并未明确指定如何转化直接左递归，只是举了个例子。可以参考编译原理了解这块内容。

间接左递归的消除，参考原文原文。基本思想是首先将间接左递归转化为直接左递归，然后再利用上面的转化方式消除直接左递归。原文首先给所有非终结符定义了一个次序，下面将通过非终结符下标大小来表明非终结符在原文定义次序中的位置。这里为了便于分析, 将原文算法拆分成两部分, 第一部分由原文算法去除 rewrite 那一行, 用来将所有间接左递归转换为直接左递归. 第二部分为一个 for 1 … n 循环, 循环体就是 rewrite 那一行, 用来转化消除所有直接左递归. 在第一部分每次外层循环开始时都有不变量：对于任意 \(A_i\)，\(A_j\)，\(A_k\)，其中 i > j > k，不存在以 \(A_j\) 为左侧符号，\(A_k\) 为右侧第一个符号的产生式。所以当第一部分结束时有: 对于任意 \(A_i\), \(A_j\)，i > j，不存在以 \(A_i\) 为左侧符号，\(A_j\) 为右侧第一个符号的产生式。所以可推出此时语法中不再存在间接左递归. 原文并未给出证明, 这里我苦思又想想了个反证法, 就是假设这时仍然存在间接左递归, 即存在 \(A_i \rightarrow A_j \beta\), \(A_j \rightarrow A_m \alpha\), \(A_m \rightarrow A_i \gamma\). 再根据之前的不变量, 此处有 i < j, j < m, m < i, 很显然矛盾了嘛. 之后再利用第二部分转换消除直接左递归之后, 就可得不再存在任何形式左递归的语法.

无回溯语法, 定义参见原文. 又称预测性语法. 判定一个语法是否是无回溯语法是可判定的, 具体如何判定下面会讲. 但是判定一个语法是否存在等价的无回溯语法是无法判定的, 即无法在有限的步骤内判定.

FIRST(A), 定义参见原文. 原文同时还给出了 FIRST() 函数的定义域以及值域, 但这里为啥把 \(\epsilon\) 也塞到定义域与值域当中的? 我觉得没啥必要. 参见原文了解 FIRST() 算法, 主要就是利用了递推公式: 对于符号串 \(s = \beta_1\beta_2...\beta_k\), FIRST(s) 就是 \(FIRST(\beta_1) \bigcup FIRST(\beta_2) \bigcup ... \bigcup FIRST(\beta_n)\), 其中 \(\beta_n\) 是 \(\beta_1\) 到 \(\beta_k\) 中第一个其 FIRST 中不包含 \(\epsilon\) 的元素.

FOLLOW(A), 定义参见原文. 求解算法同样参见原文. 其主要利用 FOLLOW(A) 等于 \(FIRST(B_1)\),…, \(FIRST(B_n)\) 的并集, 其中 \(B_1\), …, \(B_n\) 是所有在推导过程中可能出现在 A 右侧的符号.

\(FIRST^+(A \rightarrow B)\); 定义参见原文. 留意这里 \(FIRST^+\) 是针对规则定义的, 而不像 FIRST, FOLLOW 是针对终结符号, 非终结符号定义的.

无回溯语法的判定, 参见原文. 针对无回溯语法, 在自顶向下语法分析中, 结合前瞻符号以及 \(FIRST^+\) 即可直接确认唯一候选规则.

语法的化简, 即给定语法 G, 生成语法 M, 其中 L(M) 等于 L(G), 而且 M 形式更简. 常见的语法化简手段有 \(\epsilon\) 产生式擦除, 提取左因子等, 原文并未涉猎这些, 编译原理简单提到了一星半点, 所以想了解只能 Google 了. 我这里找到一篇小文章, 介绍了一些常见的语法化简手法, 可以看一看了解一下. 这篇文章定义上下文无关语法四元组使用的符号有点怪, \(G = (V; \sum ;R; S)\), 其中 V 标识非终结符; \(\sum\) 用来标识终结符; R, 用来描述规则; S 标识开始符号.

3.3.2 自顶向下的递归下降语法分析器

递归下降语法分析器; 简单来说, 就是每一个非终结符号都对应着一个函数, 该函数调用形式为: void f(word), 当函数调用时, word 为输入流中下一个待匹配的单词, f() 会从 word 开始在输入流中找到 f() 对应非终结符的一个实例, 或者说一个推导, 当 f() 返回时, 输入流中下一个待匹配的单词指针会被调整为 f() 匹配出实例的下一个位置. 可以参考原文图 3-10 了解递归下降语法分析器的具体实现姿势.

3.3.3 表驱动的 LL(1) 语法分析器

LL(1) 语法分析器, 是指哪些从左到右扫描输入, 每次都采用最左推导, 在前瞻一个符号的情况下可以做到无回溯的语法分析器. 原文并未显式表明 LL(1) 语法分析器是无回溯的, 不过根据 “LL(1) 语法是无回溯的” 这句话可以推测出 LL(1) 语法分析器也是无回溯的.

LL(1) 语法, 可以用 LL(1) 语法分析器进行语法分析的语法总称. LL(1) 语法是无回溯的. 基本上程序设计语言大部分语法结构都可以用 LL(1) 语法来描述表达.

LL(1) 表的生成算法, 以及表驱动的 LL(1) 语法分析器框架参见原文, 感觉没啥难点. 在看表驱动 LL(1) 语法分析器框架时注意在每次循环开始时都遵循的不变量, stack 栈顶符号始终是本次循环要展开或者测试的符号, 所以在压入 \(B_1, B_2, B_3, ...\) 时优先压入 \(B_k\), 最后压入 \(B_1\), 确保 \(B_1\) 是在下次循环时测试. focus 始终指向着 stack 栈顶符号. word 始终为输入流中下一个待匹配的单词.

直接编码的语法分析器, 按我理解就是上面说的递归下降语法分析器, 只不过这里是由语法分析器生成器根据用户输入的语法来自动生成的直接编码语法分析器.

3.4 自底向上语法分析

我个人觉得, 本章的章节安排的有点乱, 像是有点自顶向下的味道, 先是在未介绍 action 表, goto 表啥意思的情况下整了个 LR(1) 语法分析器框架, 然后又是整了一堆看起来吃力的概念, 比如: LR(1) 项集的规范族这些. 不过反正最后闷着头也能学下来, 虽然有点吃力. 所以我在总结本章内容时会按照知识点依赖的顺序自底向上的介绍, 希望不会让我以后再回顾看时再有吃力感, 而是有种自然而然的感觉.

自底向上语法分析是找寻最右推导的反向推导. 自底向上语法分析这个概念早在之前就已经介绍过, 那么自底向上语法分析器找寻的是最左推导的反向推导, 还是最右推导的反向推导呢? 先看下面的例子:

# 即原文图 3-16a 中的语法.
Goal -> List
List -> List Pair
    | Pair
Pair -> ( Pair )
    | ( )

# 输入串 (())() 的最左推导
Goal -> List
Goal -> List Pair
Goal -> Pair Pair
Goal -> ( Pair ) Pair
Goal -> ( () ) Pair
Goal -> (()) ()

# 输入串 (())() 的最右推导
Goal -> List
Goal -> List Pair
Goal -> List ()
Goal -> Pair ()
Goal -> ( Pair ) ()
Goal -> ( () ) ()

根据上面最左推导形式可知, 如果想要自底向上寻找最左推导, 那么需要将词法分析结果全部读取出来, 然后从输入单词流的最右侧单词开始, 不断地向左读取并进行产生式的替换. 以输入串 ‘(())()’ 为例, 从右到左开始读取, 当读取到 ‘()’ 时, 依据产生式 ‘Pair -> ()’ 将 ‘()’ 替换为 Pair 得到 ‘(()) Pair’, 然后重复这个过程依次得到 ‘( Pair ) Pair’, ‘Pair Pair’, ‘List Pair’, ‘List’, ‘Goal’.

而对于最右推导而言, 则是从输入单词流的左侧开始不断地进行读取, 替换, 最终得到完整的最右推导的反向推导, 还是以输入串 ‘(())()’ 为例, 从左到右进行读取, 替换, 依次得到 ‘(‘, ‘((‘, ‘(()’, ‘( Pair’, ‘( Pair )’, ‘Pair’, ‘Pair (‘, ‘Pair ()’, ‘Pair Pair’, ‘List Pair’, ‘List’, ‘Goal’.

即找寻最右推导的反向推导过程与词法分析单元从左到右的工作模式更为契合, 所以自底向上语法分析器找寻的是最右推导的反向推导.

句柄, 归约; 在找寻最右推导的反向推导过程中, 如果当前已读取到某个产生式右侧的所有符号, 并且输入单词流中下一个符号(后面会称呼为前瞻符号)为某个特定符号时, 可以将已读取到的产生式右侧所有符号替换为产生式左侧符号. 那么这里就是一个句柄. 注意这里成为句柄, 不光要求读取到产生式右侧所有符号, 还要求前瞻符号为特定的一个符号. 自底向上语法分析器的日常工作就是找寻句柄, 然后替换(这里的替换后面会称呼为归约), 再找寻句柄, 再归约.

LR(1) 语法分析器, LR(1) 语法; LR(1) 语法分析器是指哪些从左到右扫描输入单词流, 在仅需要一个前瞻符号的情况下, 就能自底向上的找寻到输入单词流的一个最右推导的语法分析器. 能被 LR(1) 语法分析器进行语法分析的语法则被称为具有 LR(1) 性质的语法, 不正规地简称为 LR(1) 语法. 后面会讲到这里不能被 LR(1) 语法分析器进行语法分析是种怎么样的形式. LR(k) 语法分析器是指在前瞻最多 k 个符号的前提下就能自底向上的找寻到输入单词流的一个最右推导的语法分析器. 与 LR(1) 相比, LR(k) 可以识别出更多的语法集合, 即某些语法仅能被 LR(k) 语法分析器识别, 而无法被 LR(1) 语法分析器识别. 但 LR(1) 与 LR(k) 能识别的语言集合是相同的, 即所有仅能被 LR(k) 语法分析器识别的语法总能改写使其可被 LR(1) 语法分析器识别.

LR(1) 项; LR(1) 项用来描述 LR(1) 语法分析器某一时刻的状态. LR(1) 项记为: \([A \rightarrow \beta \cdot \gamma, a]\)，其中 \(\beta\) 表明语法分析器已经读取并归约之后的信息. \(\gamma\) 表明尚未获取的消息. a 为前瞻符号. 这里语法分析器的状态可能可以同时用多种 LR(1) 项来描述, 以上面的括号语法为例, 当语法分析器处于 \([Goal \rightarrow \cdot List, eof]\) 项指定的状态时, 也可以认为语法分析器同时处于 \([List \rightarrow \cdot Pair, eof]\) 项指定的状态, 这些 LR(1) 项互为蕴含关系. 另外根据 LR(1) 项中, 占位符 \(\cdot\) 所处地位置可以将 LR(1) 项分为可能的, 部分完成的, 完成的三类, 具体定义可以参见原文.

LR(1) 项集, LR(1) 项组成的集合, 集合中的 LR(1) 项相互蕴含; 此时不再存在一个 LR(1) 项, 其不在项集中, 并且被项集中某个 LR(1) 项蕴含. 可以用原文图 3-20 中算法来根据一个核心项集求取完整项集. LR(1) 项集可以用来完整地描述语法分析器所处地状态.

LR(1) 项集, 状态转移; 状态转移用来描述语法分析器从当前所处状态跳转到下一个状态的过程. 即状态转移的输入是一个 LR(1) 项集表示当前状态, 一个符号, 可能是终结符号也可能是一个非终结符号, 对应着语法分析器从输入单词流中读取到的终结符号或者应用归约之后得到的一个非终结符号. 状态转移的输出也是一个 LR(1) 项集表明语法分析器下一个状态. 状态转移的实现参见原文图 3-21.

LR(1) 项集的规范族; LR(1) 项集的规范族的构建, 参见原文图 3-22 中算法了解. 其从一个初始状态出发, 不断应用状态转移, 最终生成一个 LR(1) 项集集合以及集合中状态之间的转移. LR(1) 项集的规范族可以用一个 DFA 来描述, DFA 的状态集合, 转移表就是规范族构造过程生成的状态集合以及转移, DFA 的初始状态就是规范族构造过程中使用的初始状态, DFA 的接受状态就是哪些存在完成的 LR(1) 项的 LR(1) 项集. 这里将 LR(1) 项集, 状态两个概念混用了, 毕竟他们指向着同一个事物.

Action, Goto 表; LR(1) 项集的规范族中每一个状态都对应着表中的一行, 上下文无关语法中的每一个终结符号对应着 Action 表中一列, 每一个非终结符号对应着 Goto 表中的一列. Action 表的任一表项记录了语法分析器在指定状态时, 遇到指定终结符号时所采取的动作, 目前有三类动作: 归约, 移进, 接受. Goto 表中表项记录了语法分析器在指定状态时, 遇到指定非终结符号时下一个状态. 这里 Action, Goto 表任一表项仅能被赋值一次. 具体参见原文图3-24中算法了解如何从 LR(1) 项集的规范族生成 Action, Goto 表. 这里不具有 LR(1) 性质的语法会无法构建 Action, Goto 表, 它们会发现可能会对 Action, Goto 表某一表项进行重复赋值, 可以参考原文 3.4.3 了解几个不具有 LR(1) 性质的语法, 以及它们在构建 Action, Goto 表表项的遇到的问题.

表驱动的 LR(1) 语法分析器框架, 参见原文图 3-15. 这里使用 stack 来记录句柄的 \(\beta\) 部分.

后语

由于这篇博文长度已经很大了, 所以后续章节的读书笔记将会放在另外一篇文章中.

参考

编译器设计, 第2版.

• Previous
  C++er 的 java 入门指南
• Next
  编译器设计读书笔记-2